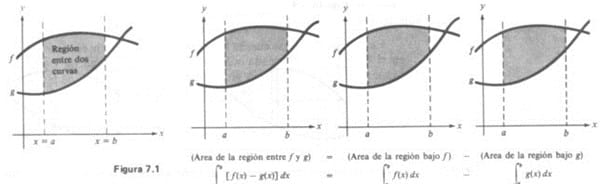
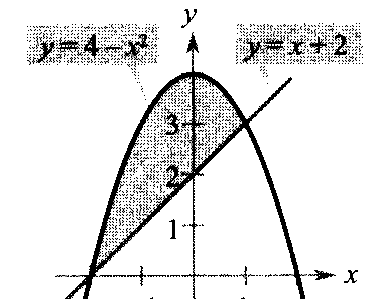
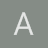¿Cómo evaluar una integral y cambiar el orden de integración?
Me pueden ayudar a integrar y cambiar el orden de integración del siguiente ejercicio:
2 Respuestas
Respuesta de Abel Rodrigo
1
Respuesta de Valero Angel Serrano Mercadal
1