Cual es la solución a este ejercicio, encontrar angulo
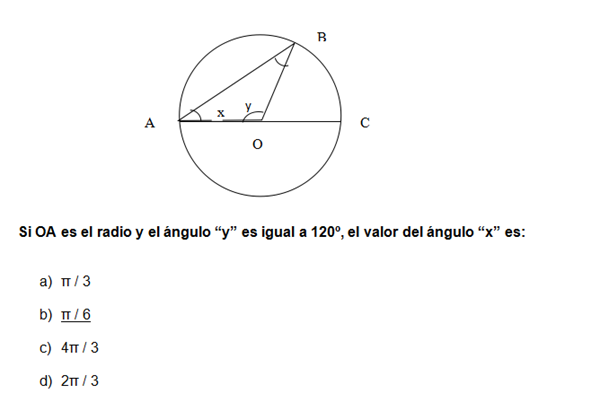
¿Alguien me explica porque es ese el resultado?
Si OA es el radio...
2 respuestas
Respuesta
2
Respuesta de Valero Angel Serrano Mercadal
2
