Resolver problema con integral definida

·

·

¡Hola Juna!

Vamos a reducir las cuentas a la sección circular, esas cuentas multiplicadas por 3 dan el volumen. Luego consideramos el cálculo del área de un sector circular de circunferencia.

Pondremos esa circunferencia sobre el eje X, para ello su ecuación será

x^2 + (y-1)^2 = 1

Supongamos que el líquido llega hasta una altura h. Calcularemos el área de ese sector circular como la suma de las cuerdas horizontales del circulo que van desde 0 hasta h. Veamos cuanto mide una de esas cuerdas en función de su altura que es el valor de la y.

$$\begin{align}&x= \sqrt{1-(y-1)^2}\\&\text{Como la cuerda va de -x a x la longitud es}\\& l=2 \sqrt{1-(y-1)^2}\\&\text{y el área del sector será}\\&\\&A=\int_0^h 2 \sqrt{1-(y-1)^2}dy=\\&\\&y-1=sen\, t\\&dy = \cos t\;dt\\&y=0\implies sen \,t=-1\implies t = - \frac \pi 2\\&y=h \implies t=arcsen(h-1)\\&\\&2\int_{-\pi/2}^{arcsen(h-1)}\sqrt{1-sen^2t}·cost\;dt=\\&\\&2\int_{-\pi/2}^{arcsen(h-1)}\cos^2t \;dt=\\&\\&2\int_{-\pi/2}^{arcsen(h-1)}\frac{1+\cos 2t}{2}dt=\\&\\&\left[t+\frac{sen2t}{2}\right]_{-\pi/2}^{arcsen(h-1)}=\\&\\&\text{Mucho cuidado, el angulo doble de }-\frac \pi 2\\&\text{es el doble de }\frac{3\pi}{2}, o\; sea\; 3\pi=\pi\\&\\&arcsen(h-1)+sen(2arcsen(h-1))+ \frac \pi 2-0=\\&\\&\text{el seno del ángulo doble es}\\&sen\, 2\alpha = 2 sen\alpha·\cos \alpha\\&\\&=arcsen(h-1)+2sen(arcsen(h-1))·\cos(arcsen(h-1))+ \frac \pi 2=\\&\\&arcsen(h-1)+2(h-1) \sqrt{1-(h-1)^2}+\frac \pi 2\\&\\&\text{Esa es el área, luego el volumen}\\&\\&V=3\left(arcsen(h-1)+2(h-1) \sqrt{1-(h-1)^2}+\frac \pi 2  \right)\\&\\&\text{Podemos comprobar que para  h=0}\\&V=3\left(arcsen(-1)-2 \sqrt 0+\frac \pi 2\right)=3\left(-\frac{\pi}{2}+\frac \pi 2  \right)=3·0=0\\&\\&\text{Para h=1 que es la mitad}\\&\\&V=3\left(arcsen(0)-2· 0 \sqrt 1+\frac \pi 2\right)=3\left(0+0+\frac \pi 2  \right)=\frac{3\pi}{2}\\&\\&\text{Para h=2  tanque completo}\\&\\&V=3\left(arcsen(1)-2· 1 \sqrt 0+\frac \pi 2\right)=3\left(\frac \pi 2+0+\frac \pi 2  \right)=3\pi\\&\end{align}$$

Y la gráfica será esta, yo no se a que herramienta se refiere, yo uso la que se usar.

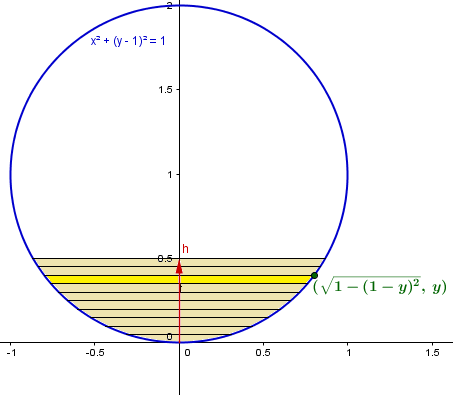
Las franjitas horizontales son las que se integran para calcular el área, es una integral entre 0 y h de la longitud de cada una que es la que ya dijimos antes, el doble de x en el punto (x, y)

Bueno yo he llamado h a lo que llamaban d en el enunciado, da lo mismo.

·

Sobre la última parte.

La marca de 1/2 está clara, en la varilla de 2metros estaría en 1 metro.

Para la marca de 1/4 debes resolver la ecuación

$$\begin{align}&arcsen(h-1)+2(h-1) \sqrt{1-(h-1)^2}+\frac \pi 2=\frac \pi 4\\&\\&arcsen(h-1)+2(h-1) \sqrt{1-(h-1)^2}+\frac \pi 4=0\end{align}$$

Yo no sé cómo se hará con esa calculadora, lo he intentado y me da respuestas falsas.  Pero si vas a la página de WolframAlpha y escribes en la caja

arcsen(h-1)+2(h-1)sqrt(1-(h-1)^2)+pi/ 4=0

te dará la respuesta.

Voy a escribir el enlace pero ya se que no sera clicable porque esta página va mal, deberías escribir el enlace en tu barra de direcciones

http://www.wolframalpha.com/input/?i=arcsen%28h-1%29%2B2%28h-1%29sqrt%281-%28h-1%29^2%29%2Bpi%2F+4%3D0 

Y el resultado es

h=0.732820536

Y para 3/4 la ecuación a escribir será

arcsen(h-1)+2(h-1)sqrt(1-(h-1)^2)-pi/ 4=0

y el resultado

h= 1.267179464

Que como puedes ver es simétrico del anterior respecto a 1, lo cual está bien.

¡Ah por cierto! Vamos a hacerlo más general. Si en vez de radio 1 es radio R, la formula del volumen la multiplicas por R^2 y te sirve. Por supuesto que si la longitud del cilindro es ditinta de 3 cambias el 3 por la longitud verdadera.

·

Saludos

·

·

No, quita lo de que se multiplica por R^2 y ya está, en realidad hay que hacer más cosas. Si hubiéramos empezado el ejercicio con un radio genérico habríamos deducido la fórmula para cualquier radio con un pelín más de esfuerzo, pero como nos decían que el radio era 1 nos desentendimos de poner uno genérico.

Saludos.

:

:

¡Gracias! muchas gracias valeroasm