Límites de funciones calculo diferencial
Ayuda a resolver los siguientes ejercicios de límites de funciones y continuidad:
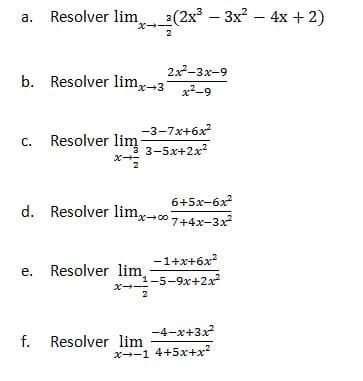
3 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta
2
Respuesta
1

