Hallar el siguiente problema de programación lineal:
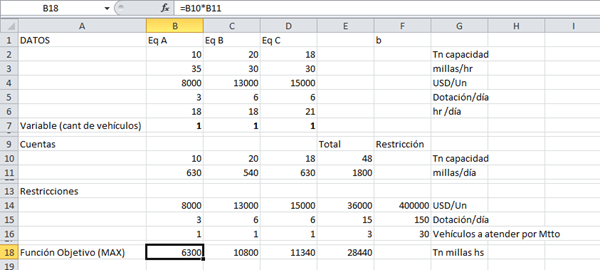
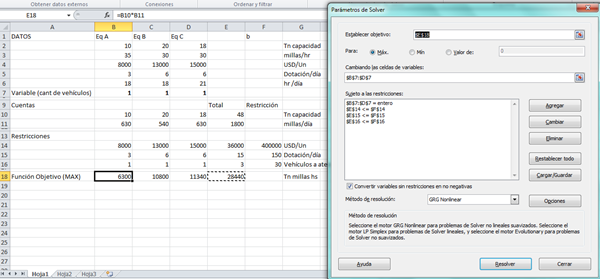
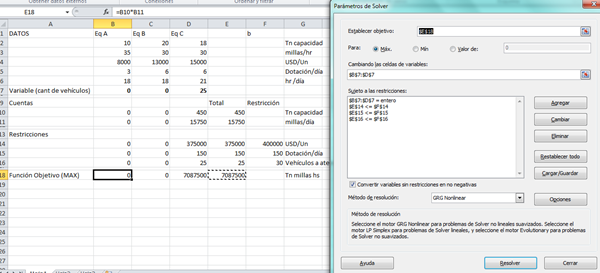
Una compañía de transporte dispone de 400,00 dolares para comprar equipo nuevo, y en ese sentido esta considerando la adquisición de 3 tipos de vehículos .
El vehículo A puede transportar 10 toneladas con una velocidad promedio de 35 millas por hora, siendo su costo unitario de 8000 mil dolares.
El vehículo B tiene una capacidad de 20 tonelada con una velocidad promedio de 30 milla por hora y vale 13000 mil dolares la unidad.
El vehículo C es un modelo modificado del vehículo B, teniendo un lugar para que duerma un chófer, lo cual reduce su capacidad de carga en 18 toneladas, siendo su costo de 15000 mil dolares la unidad.
El vehículo A requiere una tripulación de una persona, operando 3 turnos al día para trabajar con un promedio de 18 horas diarias. Los vehículos B y C requieren una tripulación de dos hombres cada un, mientras el vehículo B puede trabajar 18 horas diarias en 3 turno, el vehículo C puede trabajar 21 horas diarias en los tres turnos.
La compañía dispones 150 chóferes
Diarios y ya no tiene posibilidades económicas para contratar tripulación adicional, por otro lado la facilidades de mantenimiento de esa empresa no puede atender a más de 30 vehículos.
Cuantos vehículos de cada tipo deben comprarse, sabiendo que la compañía desea maximizar su capacidad operativa la cual se mide en tonelada, milla por hora .
Nota: que lo resuelva con toda sus restricciones
2 Respuestas
Yo lo resolví con el Solver del Excel y llego a la solución que a mejor opción es comprar 25 vehículos tipo C
Planteo Inicial
Planteo en Solver
Solución hallada
·
Veamos primero cuál es la función objetivo:
Es conseguir el mayor número de toneladas movidas el mayor número de millas, eso es lo que entiendo yo, la verdad que no lo veo muy claro.
Entonces si compra a, b, c vehiculos de las respectivas clases A, B, C la función objetivo es
F(a,b,c) = 10·35·18·a + 20·30·18·b + 18·30·21·c
F(a,b,c) = 6300a + 10800b + 11340 c
Y las restricciones son estas.
Vehículos que puede mantener
a+b+c <= 30
Precio vehículos
8000a + 13000b + 15000c <= 400000
Operarios y turnos
3a + 6b + 6c <= 150
Y lo dejo aquí, si la función objetivo fuera de dos variables lo podría resolver gráficamente, pero funciones de más variables no recuerdo como se hacían.
Saludos.
:
: