Problemas con integrales, calculo integral
Solucionar el siguiente problema para resolver la Integral indefinida y evaluar sus intervalos dados
1 Respuesta
·
·
¡Hola Cristal!
Usaremos exponentes negativos para llevar todo al numerador y poder usar la típica integral inmediata de los monomios.
$$\begin{align}&\int x^ndx = \frac{x^{n+1}}{n+1} \qquad Si\; n\neq -1\\&\\&\\&\int_{-3}^1 \left(\frac 1{x^2}-\frac 1{x^3}\right)dx=\int_{-3}^2(x^{-2}-x^{-3})dx=\\&\\&\left[\frac{x^{-1}}{-1}-\frac{x^{-2}}{-2} \right]_{-3}^1=\left[-\frac 1x+\frac 1{2x^2} \right]_{-3}^1=\\&\\&\text{mucho cuidado con los signos, a veces hay 3 signos -}\\&\\&-\frac{1}{1}+\frac{1}{2·1^2}+\frac{1}{-3}-\frac{1}{2(-3)^2}=\\&\\&-1+\frac 12-\frac 13-\frac{1}{18}=\frac{-18+9-6-1}{18}=\\&\\&-\frac{16}{18}=-\frac{8}{9}\end{align}$$Bueno, esa es la respuesta que probablemente quiere el profesor que pongas. Pero en realidad esta integral no existe es divergente, pero eso es de niveles superiores, si acaso se lo puedes comentar.
Saludos.
:
:
Espera, a lo mejor he supuesto que no has dado integrales convergentes y divergentes y sí las has dado. Si las has dado sabrás que esa integral se debe dividir en dos trozos porque en 0 se hace infinita. Y en los dos trozos la integral impropia es divergente.
El segundo teorema fundamental del cálculo o regla de Barrow que dice que la integral definida es el valor de la integral indefinida en el extremo superior menos el valor en el inferior sirve para funciones continuas en el intervalo de integración. Pero esta función tiene el 0 en el intervalo de integración donde la función tiende a infinito. Lo que pasa frecuentemente a quien crea los ejercicios de integrales es que no se da cuenta de eso y piensa qe se puede usar la regla.
La integral bien hecha en este caso requiere dividirla en dos trozos y calcular los límites.
Partiendo de la indefinida que ya hemos resuelto sería:
$$\begin{align}&\left[-\frac 1x+\frac 1{2x^2} \right]_{-3}^0+\left[-\frac 1x+\frac 1{2x^2} \right]_{0}^1=\\&\\&\text{En 0 deben tomarse los límites izquierdo en el}\\&\text{primer sumando y el derecho en el segundo}\\&\\&\lim_{x\to 0^-}\left(-\frac 1x+\frac 1{2x^2} \right)=\\&\\&\lim_{x\to 0^-}\left(\frac {-2x+1}{2x^2} \right)=\frac{1}{0^+}=+\infty\end{align}$$Luego el primer corchete vale +infinito. Y puedes comprobar que el siguiente vale -infinito. Pero no son dos infinitos compensables ya que la función no es simetrica respecto al punto (0,0) luego no se pueden anular así como así.
Que bueno, tu sabrás que hacer con el ejercicio. Si no has dado integrales impropias seguramente que lo mejor es que te olvides de todo y pongas la respuesta -8/9. Y si las has dado o si quieres que se sepa le dices al profesor que es un integral impropia y no se puede aplicar la regla de Barrow.
Saludos.
:
:
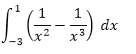
Comentario borrado por el autor - Abi Herrera
Disculpe como se resolvió a parte de los intervalos, que parte es esa? - Abi Herrera