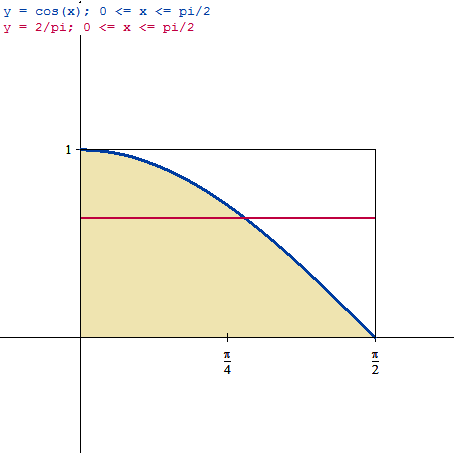
Calcular el valor promedio de la función en el intervalo dado
Calcular y graficar el valor promedio de la siguiente función en el intervalo dado
Ejercicio 1:
 Calcula el valor promedio de la función en el intervalo dado
Calcula el valor promedio de la función en el intervalo dado
2 Respuestas
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1