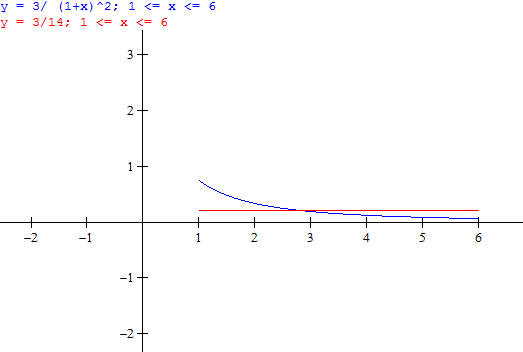
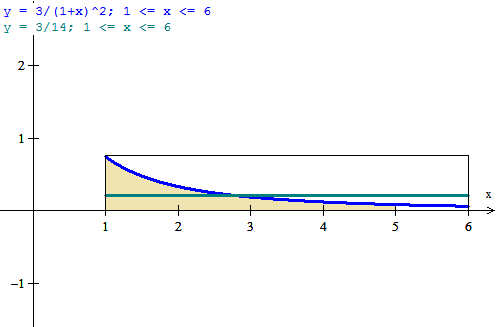
Problema de calculo integral valor promedio
Calcula el valor promedio de la función en el intervalo dado.
Gráfica y checa el valor promedio a partir de la gráfica dada, para graficar checa en las diapositivas como se realiza .
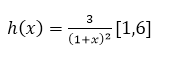
2 respuestas
Respuesta
1
Veamos...
$$\begin{align}&\overline{h(x)} = \frac{1}{6-1} \int_1^6 \frac{3}{(1+x)^2} dx = \\&\frac{3}{5} \int_1^6 (1+x)^{-2} dx = \\&\frac{3}{5} \frac{(1+x)^{-1}}{-1} \bigg|_1^6 = \frac{-3}{5} \bigg(\frac{1}{(1+x)} \bigg|_1^6 \bigg) =\\&\frac{-3}{5} \bigg(\frac{1}{(1+6)}-\frac{1}{(1+1)} \bigg) =\\&\frac{-3}{5} \bigg(\frac{1}{7}-\frac{1}{2} \bigg) =\frac{-3}{5} \cdot \frac{-5}{14}=\frac{3}{14}\end{align}$$Te dejo la gráfica
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Cristal!
El valor promedio de la función en un intervcalo es la integral en ese intervalo dividida entre la longitud del intervalo.
$$\begin{align}&\overline{f_{[a,b]}}=\frac{\int_a^b f(x)dx}{b-a}\\&\\&\overline{g_{[0,\frac \pi 2]}}= \frac{1}{6-1}\int_1^6 \frac{3dx}{(1+x)^2}=\frac 35\int_1^6(1+x)^{-2}dx=\\&\\&\frac 35·\frac{(1+x)^{-1}}{-1}\bigg|_1^6=-\frac 35·\frac{1}{1+x}\bigg|_1^6=\\&\\&-\frac 35\left(\frac 17 -\frac 12 \right)=-\frac 35·\frac{(2-7)}{14}=\frac 3{14}\\&\end{align}$$Y esta es la gráfica:
Y eso es todo, saludos.
:
: