Actividad de calculo área entre las curvas

Te dejo la gráfica

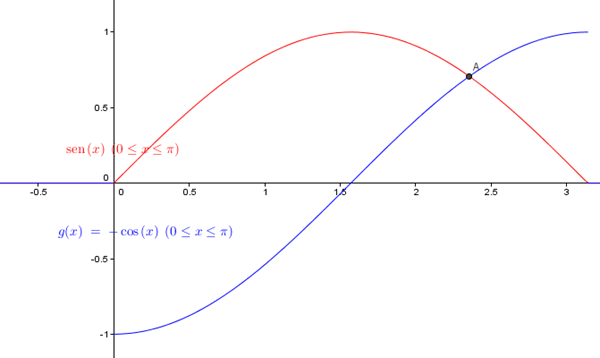
Se ve que entre 0 y el punto "A" es la función seno - (-coseno) y luego la función -coseno está por arriba del seno. Así que tendremos que partir la integral, pero antes vamos a calcular el punto "A"

Sabemos que sen (x) = cos (x) en 45° y en 225°, y que

sen(x) = -cos (x) en 135° y en 315°. Como estamos entre 0 y PI el valor es 135° que expresado en radianes es 3/4 PI

Ahora hagamos los cálculos del área:

$$\begin{align}&Area = \int_0^{3/4 \pi } senx - (-cosx) dx + \int_{3/4 \pi}^{\pi} -\cos x - sen x \ dx = \\& \int_0^{3/4 \pi } senx + cosx\ dx - \int_{3/4 \pi}^{\pi} \cos x + sen x \ dx = \\&(-\cos x + senx ) \bigg|_0^{3/4 \pi } -  (sen x -\cos x) \bigg|_{3/4 \pi}^{\pi} = \\&\bigg((-\cos (3/4 \pi) + sen (3/4 \pi) )-(-\cos(0) + sen (0) )\bigg)  - \bigg(  (sen (\pi) -\cos (\pi)) - (sen (3/4 \pi) -\cos (3/4 \pi)) \bigg) =\\&\bigg((-(\frac{-\sqrt 2}{ 2}) + \frac{\sqrt 2}{ 2}) )-(-1 + 0 )\bigg)  - \bigg(  (0 - (-1)) - (\frac{\sqrt 2}{ 2} - (\frac{-\sqrt 2}{ 2})) \bigg) =\\&\bigg(\sqrt 2+1 \bigg)  - \bigg(  1 -  \sqrt 2 \bigg) =\\&\sqrt 2+1 - 1 +  \sqrt 2=2 \sqrt 2\end{align}$$

Hice todos los pasos en la resolución de la integral pero por las dudas revisá las cuentas porque pude haber errado en algún paso (sobre todo con tantos signos dando vueltas)

Disculpe ¿por que mi gráfica hecha en geogebra dice que el área e igual a 2?