Problema con ejercicio de conservación de la energía
Tengo problemas coneste ejercicio
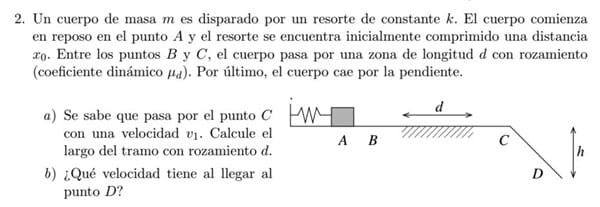
No se como calcular el tramo con rozamiento
Espero me puedan ayudar por que tengo parcial mañana :D.
3 Respuestas
Respuesta de Gera Gorgoretti
1
Respuesta de Valero Angel Serrano Mercadal
2
Respuesta de Instalaciones Salvador
-1

