¿Cómo determinar los extremos relativos, puntos de inflexión y graficar?

;)
Hola Ignacio!

Te hago el segundo:

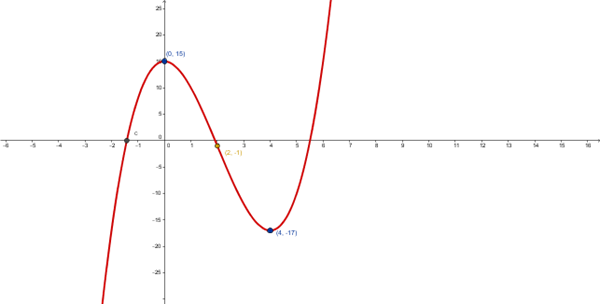
$$\begin{align}&y=x^3-6x^2+15\\&\\&Puntos \ críticos : y'=0\\&\\&y'=3x^2-12x\\&\\&3x^2-12x=0\\&3x(x-4)=0\\&x_1=0\\&x_2=4\\&intervalos \ crecimiento:\\&(- \infty,0) \rightarrow y'(-10)300-120>0 \rightarrow creciente\\&(0,+4) \rightarrow y'(1)=3-12<0 \rightarrow decreciente\\&(4,+ \infty) \rightarrow y(10)=300-120>0 \  creciente\\&\\&Max ximo \ relativo (0,f(0))=(0,15)\\&mínimo \ reltivo (4,f(4))=(4,-17)\\&f(4)=4^3-6·4^2+15=-17\\&\\&puntos \ inflexión \Rightarrow   y''=0\\&\\&y''=6x-12\\&\\&6x-12=0\\&x=2\\&Punto Inflexión (2,f(2))=(2,-1)\\&\\&\end{align}$$

Por el Teorema de Bolzano:

f(x) es contínua al ser Polinómica

f(-3)=-27-54+15 <0

f(0)=15 >0

cambia de signo ===> existe c en  [-3,0] tal que f(c)=0

Saludos

;)

;)