Lirio, antes de responder tu pregunta, te hago un par de consultas para que me aclares e intentemos resolver el ejercicio juntos:
1. Te piden el método óptimo, ¿o te "alcanza" con una aproximación?
2. Sabés que aunque se trate de programación lineal (PL), ¿en realidad estos problemas son más específicos y se modelan como "modelo de transporte" o "algoritmos de transporte"?
3. ¿Qué métodos conoces?
Inicialmente para ayudarte en tus respuestas, te diré que hay 3 métodos (por lo menos) de aproximación y al menos un método de solución óptima, los métodos son:
- Esquina Noroeste: aproximación
- Costo mínimo: aproximación
- Aproximación de Vogel: aproximación
- Método de multiplicadores: solución óptima
Además de resolver el problema directamente como PL directamente con Simplex o, si se puede, por método gráfico.
Hasta que me respondas tus preguntas, te voy a resolver el algoritmo por el método de esquina noroeste, ya que es muy fácil de implementar (recuerda que no es óptimo).
El planteo inicial, es independiente del método utilizado y te lo dejo a continuación:
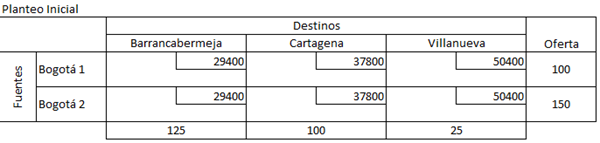
Lo primero que hay que hacer es asegurar que las sumas de las ofertas estén balanceadas con las sumas de las demandas (en este caso ambas dan 250 y están balanceadas)
Para esquina noroeste, comenzás por la esquina superior derecha y colocás el mínimo entre la oferta y la demanda (en este caso 100 de oferta), esto descartará toda una fila o columna (en este caso fila) y volvés a plantear el algoritmo con lo que queda (ajustando la oferta y la demanda, afectadas por el punto anterior). Te dejo el paso a paso de este método porque es elemental que lo entiendas para después poder profundizar con otros métodos.
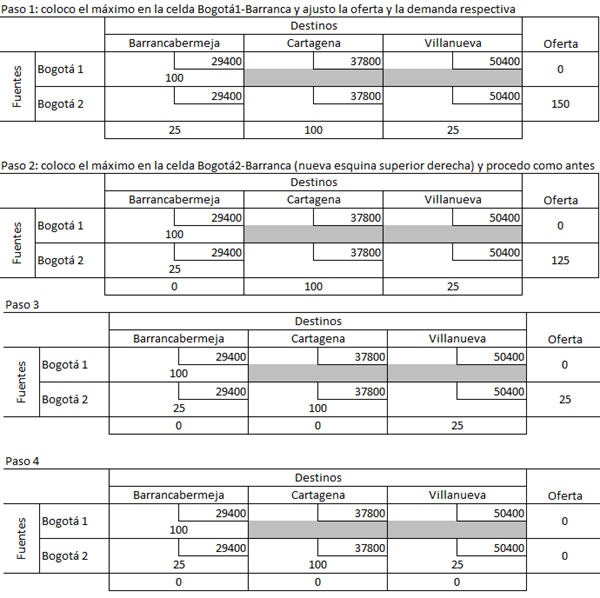
Quedaría calcular el costo de esta función (que no tiene por qué ser mínimo, pues ya dijimos que este método no es óptimo)
z = 100*29400 + 25 * 29400 + 100*37800 + 25 * 50400 = 8715000
Igualmente, viendo los costos individuales entre cada par de nodos, creo que no hay nada que se pueda optimizar, porque a cada destino cuesta lo mismo no importa cual sea la fuente