Área triángulo dado un punto, coordenadas -analítica

·

·

¡Hola Llaq!

¡Milagro! Herrera a descubierto la fórmula del área del triángulo. Ahora a ver que día se da el milagro y se decide a resolver algún problema.

Hallamos la ecuación genérica de una recta que pasa por el punto (3,2)

y-2 = m(x-3)

Donde m es la pendiente.

Los cortes de esta recta con los ejes son:

Con el eje X cuando y=0

-2 = m(x-3)

-2 = mx - 3m

mx = 3m-2

x = 3 - 2/m

Con el eje Y cuando x=0

y-2 = m(0-3)

y =2-3m

Y el área que forman es

$$\begin{align}&A=\frac{\left|  \left(3-\frac 2m  \right)(2-3m)\right|}{2}=12\\&\\&\left| 6-9m-\frac 4m+6 \right|=24\\&\\&\left|12 -9m -\frac{4}{m}\right|=24\\&\\&\text{Esto son dos ecuaciones:}\\&\text{La primera tomando positivo el interior}\\&\\&12-9m -\frac 4m = 24\\&\\&9m+\frac 4m+12=0\\&\\&\text{multiplico por m}\\&\\&9m^2+12m+4=0\\&\\&(3m+2)^2=0\\&\\&3m+2=0\\&\\&m=-\frac 23\\&\\&\text{Luego la primera recta es}\\&\\&r_1:\quad y-2=-\frac 23(x-3)\\&\\&r_1:\quad3y-6=-2x+6\\&\\&r_1:\quad2x+3y-12=0\\&\\&\text{Y la otra ecuación tomando el interior negativo}\\&\\&-12+9m +\frac 4m = 24\\&\\&9m+\frac 4m-36=0\\&\\&\text{multiplico por m}\\&\\&9m^2-36m+4 = 0\\&\\&m=\frac{36\pm \sqrt{36^2-4·9·4}}{18}=\frac{36\pm 24 \sqrt 2}{18}=\frac{18\pm 12 \sqrt 2}{9}\\&\\&\text{Y esto nos dará otras dos rectas}\\&\\&y-2=\left(\frac{18\pm 12 \sqrt 2}{9} \right)(x-3)\\&\\&9y-18=(18\pm 12 \sqrt 2)x-54\mp 36 \sqrt 2\\&\\&(18\pm 12 \sqrt 2)x -9y -36 \mp 36 \sqrt 2=0\\&\\&r_2:\quad (18+12 \sqrt 2)x -9y -36 - 36 \sqrt 2=0\\&\\&r_3:\quad (18- 12 \sqrt 2)x -9y -36 + 36 \sqrt 2=0\end{align}$$

Y esta es la comprobación.

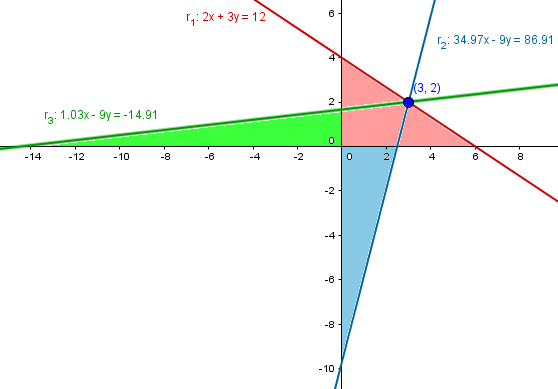
Y esa es la respuesta de verdad, es decir tres rectas. Espero que después de esto valores las respuestas de los dos que debes valorar y no des ni un punto ni medio al vago de siempre.

S a l u d o s.

:

:

Aquí encontrarás la respuesta:

https://www.youtube.com/watch?v=Wt0vX1jJitE 

https://www.youtube.com/watch?v=uQ2kmY7-NPw 

https://www.youtube.com/watch?v=kJPCL95LYas 

Hola Jorge Herrera.

No me ayudan esos vídeos.

Yo he obtenido una de las ecuaciones (la más fácil), tomando como extremos las intersecciones con el eje Y y con el eje X, de la recta que pasa por el punto (3,2), pero en el libro dan 3 ecuaciones como respuestas y no sé cómo obtenerlas.

Es decir, que existen al menos tres rectas que pasan por el punto (3,2), las cuals forman tres triángulos diferentes de área 12.

Primera ecuación Y= -2/3x +4

Se me escapa algo y no sé qué es.