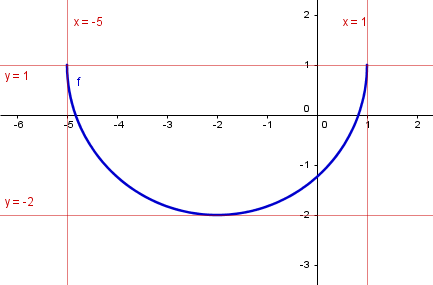
Encontrar el dominio y recorrido de f(x)=1-√ (5-4x-x^2)
Determine el dominio y me dio como resultado [-5,1] y su recorrido me dice que toma el punto 1 en el eje y, y tengo de respuesta de que mi recorrido es [1,4], saque el vértice, ya que es una parábola con una discrminante cuyo valor es menor a 0, por lo tanto no toca al eje por . Quiero saber como puede definir ese intervalo [1,4] o como puedo llegar a eso
Respuesta de Valero Angel Serrano Mercadal
2
1 respuesta más de otro experto
Respuesta de Jorge Herrera
-1