$$\begin{align}& \end{align}$$·
·
¡Hola José de Jesús!
Dos rectas y dos parábolas, es bastante complicado de resolver sin hacer la gráfica.
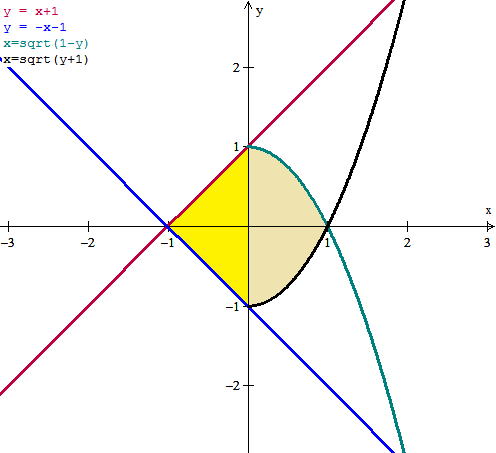
Ahora esta bien claro. Podríamos asumir que es simétrica respecto al eje POR, pero por no demostrarlo haremos las integrales enteras. Son dos integrales, una entre x=-1 y x=0, y la otra entre x=0 y x=1.
Y ahora que lo veo, la parte entre x=0 y x=1 la vamos a dividir a su vez en otras dos inferior y superior para no tener que cambiar las funciones de raíz cuadrada a sus inversas. Todo esto se puede discutir, sobre todo lo de las simetrías que no voy a utilizar, pero yo no sé como acostumbra a hacerlo tu profesor y como aquí no se puede explicar muy bien las cosas y yo nunca digo que algo es simétrico solo por verlo sin demostrarlo analíticamente, esta es la forma en la que lo hago.
$$\begin{align}&A=\int_{-1}^0\int_{-x-1}^{x+1}dy\,dx+\int_{-1}^0\int_0^{\sqrt{y+1}}dx \,dy+\\&\qquad+\int_0^1\int_0^{\sqrt{1-y}}dx\,dy=\\&\\&\int_{-1}^0(x+1+x+1)dx+\int_{-1}^0 \sqrt{y+1}\;dy+\\&+\int_0^1 \sqrt{1-y}\;dy=\\&\\&\left[x^2+2x \right]_{-1}^0 + \frac 23 (y+1)^{\frac 32}\bigg|_{-1}^0-\frac 23(1-y)\bigg|_0^1=\\&\\&-1+2+\frac 23+\frac 23=1+\frac 43=\frac 73\end{align}$$Y eso es todo.
S a l u d o s.
:
:

