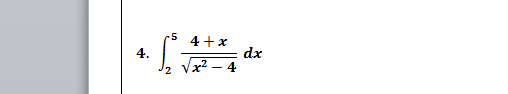·
·
¡Hola Jaime!
Menos mal que dices que es impropia porque es algo que no solemos fijarnos. Es impropia porque en 2 la función tiende a infinito. Entonces por definición será
$$\begin{align}&\int_2^5 \frac{4+x}{\sqrt{x^2-4}}dx=\lim_{k\to 2^+}\int_k^{5}\frac{4+x}{\sqrt{x^2-4}}dx\\&\\&\text{Mira, esto se resuelva con un cambio hiperbólico,}\\&\text{con uno trigonométrica es un martirio.}\\&\text{De momento calcularemos la indefinida solo}\\&\\&\int \frac{4+x}{\sqrt{x^2-4}}dx =\\&\\&x=2\;cosh\, t \implies t=arg\,cosh \frac x2\\&dx = 2\,senh\,t\;dt\\&\\&=\int \frac {4+2cosh\,t}{\sqrt{4cosh^2t-4}}·2senh\,t\;dt=\\&\\&\int \frac{4+2cosh\,t}{2 \sqrt{cosh^2t-1}}·2senh\,t\;dt=\\&\\&\int \frac{4+2cosh\,t}{\sqrt{senh^2t}}·senh\,t\;dt=\\&\\&\int(4+2cosht)dt=\\&\\&4t+2senht=\\&\\&4\,arg\,cosh \frac x2+2 senh\left(arg\,cosh \frac x2\right)=\\&\\&4·ln\left(\frac x2+\sqrt{\left(\frac x2\right)^2-1} \right)+2senh\left(arg\,senh \sqrt{\left(\frac x2 \right)^2-1} \right)=\\&\\&2ln(x+\sqrt{x^2-4}) +2 \sqrt{\left(\frac x2 \right)^2-1}=\\&\\&2ln(x+\sqrt{x^2-4})+\sqrt{x^2-4}\\&\\&\text{Y ahora evaluamos el límite}\\&\\&\int_2^5 \frac{x+4}{\sqrt{x^2-4}}= \lim_{k\to 2^+}\left[ 2ln(x+\sqrt{x^2-4})+\sqrt{x^2-4}\right]_k^5=\\&\\&2ln(5+\sqrt{21})+\sqrt{21}-2\,ln\,2\\&\end{align}$$Y eso es todo. Si acaso te dejo el enlace donde puedes ver como son las utilísimas funciones hiperbólicas. Te aparecerá automáticamenteparte del artículo y algún sitio donde pinchar para verlo completo
https://es.wikipedia.org/wiki/Funci%C3%B3n_hiperb%C3%B3lica
Y ya está.
Salu dos.
:
.
·