Tengo una duda sobre un ejercicio de Investigación de Operaciones
Me pueden apoyar a resolver el siguiente ejercicio:
Se procesan cuatro productos sucesivamente en dos máquinas. Los tiempos de manufactura en horas por unidad de cada producto se tabulan a continuación para las dos máquinas:
El costo total de producir una unidad de cada producto está basado directamente en el tiempo de máquina. Suponga que el costo por hora para las máquina 1 y 2 es $10 y $15. Las horas totales presupuestadas para todos os productos en las máquina 1 y 2 son 500 y 380. Si el precio de venta por unidad para los productos 1, 2, 3 y 4 en $65, $70, $55 y $45, formule el problema como modelo de programación lineal para maximizar el beneficio neto total.
Solución:
¿Qué es lo que vamos a Maximizar?
x1 = la Cantidad a fabricar del producto 1
x2 = la Cantidad a fabricar del producto 2
x3 = la Cantidad a fabricar del producto 3
x4 = la Cantidad a fabricar del producto 4
Realizar análisis de sensibilidad:
a) cambios en el vector de disponibilidad
b) cambios en los coeficientes tecnológicos
c) adición de una variable
Max Z = 65x1 + 70x2 + 55x3 + 45x4…….(1)
Sujetos a:
2x1 + 3x2 + 4x3 + 2x4 < 500
3x1 + 2x2 + 1x3 + 2x4 < 380
x1, x2, x3, x4 > 0
1 Respuesta
Francisco, hay algo mal en el enunciado, o el problema queda "demasiado" trivial, ya que la función objetivo NO debería ser la venta (que es lo que vos definiste como Z), sino que debería ser la utilidad que sale restando al precio de venta los costos (por uso de las máquinas). Dicho esto la utilidad para cada producto es:
x1: 65 - 2*10 - 3*15 = 0
x2: 70 - 3*10 - 2*15 = 10
x3: 55 - 4*10 - 1*15 = 0
x4: 45 - 2*10 - 2*15 = -5
Por lo que el único que tiene utilidad positiva es el producto 2, y fabricar el resto de los productos no tiene sentido hacerlos.
Revisá bien los enunciados para ver si seguimos con esto.
Lo puede usted realizar por favor así como lo dice? Ya que lo que necesito saber es cómo hacer el problema de primal a dual y realizar el análisis de sensibilidad.
Ok Francisco, igualmente hasta mañana no lo voy a poder hacer, pero aprovecho para preguntar si querés que calcule el ejercicio con la función Z que te dije yo, ¿o con la que vos ponés en el enunciado?
Con la que puse yo en el enunciado por favor
Te dejo la solución al problema
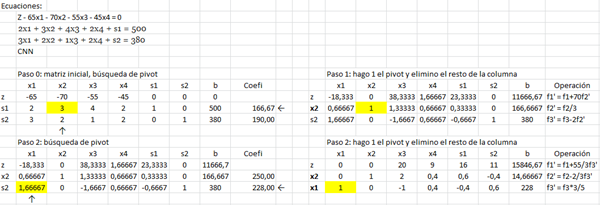
Como ves, luego del segundo paso no quedan coeficientes positivos en la función z, por lo tanto el problema termina y la solución es:
z = 15846.67, x1= 228, x2=14.67, x3=x4=0
Sensibilidad: no se como te lo explicaron a vos, y acá podemos tener inconsistencias pero bueno, te lo resuelvo "a mi modo" y cualquier cosa pregunta.
Cambio en las restricciones:
a) Que pasa si la primer restricción (de 500), ¿cambia en T? La primer restricción está asociada a la variable s1, vemos en la última tabla del simplex que valores tiene s1 y vemos que la matriz es
s1 b b + s1*T
16 15846.67 15846.67 + 16T
0.6 14.67 14.67 + 0.6T
-0.4 228 228 - 0.4T
La última columna debe ser >=0, de donde sale que
15846.67 + 16T >= 0 Entonces T >= -15846.67 / 16 = -990.42
14.67 + 0.6T >= 0 Entonces T >= -14.67 / 0.6 = -24.44
228 - 0.4T >= 0 Entonces T <= 228 / 0.4 = 570
Juntando estas condiciones de T, sale que T está en el rango [-24.44 ; 570], por lo tanto la primer restricción la podemos variar en el rango [500-24.44 ; 500+570] = [475.56, 1070] sin que cambie la solución
Análogamente, para la segunda restricción tenemos que:
b) Que pasa si la segunda restricción (de 380), ¿cambia en T? Esta restricción está asociada a la variable s2, vemos en la última tabla del simplex que valores tiene s2 y vemos que la matriz es
s2 b b + s2*T
11 15846.67 15846.67 + 11T
-0.4 14.67 14.67 - 0.4T
0.6 228 228 + 0.6T
La última columna debe ser >=0, de donde sale que
15846.67 + 11T >= 0 Entonces T >= -15846.67 / 11 = -1440.61
14.67 - 0.4T >= 0 Entonces T <= 14.67 / 0.4 = 36.67
228 + 0.6T >= 0 Entonces T >= -228 / 0.6 = -380
Juntando estas condiciones de T, sale que T está en el rango [-380 ; 36.67], por lo tanto la segunda restricción la podemos variar en el rango [380-380 ; 380+36.67] = [0 ; 410.67] sin que cambie la solución
Ahora voy a cambiar los coeficientes de la función objetivo. Empiezo por x1 (a la matriz, ahora hay que verla "cruzada")
s1 s2 b
z 16 11 15846.67
x1 -0.4 0.6 228
z + T x1 16 - 0.4T 11 + 0.6T 15846.67 + 228T
De la última fila tenemos que:
16 - 0.4T >=0 Entonces T<= 16 / 0.4 = 40
11 + 0.6T >=0 Entonces T>= -11 / 0.6 = -18.33
15846.67 + 228T >=0 Entonces T>= - 15846.67 / 228 = -69.5
De estas condiciones sale que T está en el intervalo [-69.5 ; 40] por lo que los valores posibles de x1 son [65 - 69.5 ; 65 + 40] = [0 ; 105] (el parámetro de la izquierda sería negativo, pero también debe cumplirse las "condiciones de no negatividad")
Ahora cambio x2
s1 s2 b
z 16 11 15846.67
x2 0.6 -0.4 14.67
z + T x2 16 + 0.6T 11 - 0.4T 15846.67 + 14.67 T
De la última fila tenemos que:
16 + 0.6T >=0 Entonces T>= -16 / 0.6 = -26.67
11 - 0.4T >=0 Entonces T<= 11 / 0.4 = 27.5
15846.67 + 14.67T >=0 Entonces T>= - 15846.67 / 14.67 = -1080.45
De estas condiciones sale que T está en el intervalo [-26.67 ; 27.5] por lo que los valores posibles de x1 son [70 - 26.67 ; 70 + 27.5] = [43.33 ; 97.5]
Las variables x3, x4 no forman parte de la solución.