Las secciones cónicas en la geometría analítica.
Pongo la siguiente imagen adjunta que definen las instrucciones a considerar:
Saludos.
3 Respuestas
·
·
¡Hola Mat!
Estos ejercicios llevan trabajo, deberías mandarlos de uno en uno
a) Completamos cuadrados
$$\begin{align}&\left(x+\frac 32\right)^2-\frac 94 +\left(y+ \frac 52\right)^2-\frac{25}{4}+2=0\\&\\&\left(x+\frac 32\right)^2+\left(y+ \frac 52\right)^2=\frac 94+\frac{25}4-2\\&\\&\left(x+\frac 32\right)^2+\left(y+ \frac 52\right)^2=\frac{9+25-8}{4}\\&\\&\left(x+\frac 32\right)^2+\left(y+ \frac 52\right)^2=\frac{26}{4}\\&\\&\text{Es una circunferencia}\\&\\&Centro = \left(-\frac 32-\frac 52 \right)\\&\\&Radio = \frac{\sqrt{26}}{2}\\&\\&\\&b)\quad \left(x-\frac 32 \right)^2- \frac 94+3\left(y^2+\frac y3 \right)+1=0\\&\\&\left(x-\frac 32 \right)^2- \frac 94+3\left(\left(y+\frac 16\right)^2-\frac 1{36} \right)+1=0\\&\\&\left(x-\frac 32 \right)^2- \frac 94+3\left(y+\frac 16\right)^2-\frac 1{12} +1=0\\&\\&\left(x-\frac 32 \right)^2+3\left(y+\frac 16\right)^2=\frac 94+\frac 1{12}-1\\&\\&\left(x-\frac 32 \right)^2+3\left(y+\frac 16\right)^2=\frac{27+1-12}{12}\\&\\&\left(x-\frac 32 \right)^2+3\left(y+\frac 16\right)^2=\frac{16}{12}=\frac 43\\&\\&\frac{\left(x-\frac 32 \right)^2}{\frac{4}{3}}+\frac{3\left(y+\frac 16\right)^2}{\frac 43}=1\\&\\&\frac{\left(x-\frac 32 \right)^2}{\frac{4}{3}}+\frac{\left(y+\frac 16\right)^2}{\frac 49}=1\\&\\&\text{Es una elipse}\\&\\&Centro= \left( \frac 32,-\frac 16 \right)\\&\\&Semieje \;a= \frac{2}{\sqrt 3}= \frac{2 \sqrt 3}{3}\\&\\&Semieje\; b = \frac 23\\&\\&\text{Vértice 1 }=\left(\frac 32+\frac{2 \sqrt 3}{3},-\frac 16 \right)=\left(\frac{9+4 \sqrt 3}{6},-\frac 16 \right)\\&\\&\text{Vertice 2}=\left(\frac 32-\frac{2 \sqrt 3}{3},-\frac 16 \right)=\left(\frac{9-4 \sqrt 3}{6},-\frac 16 \right)\\&\\&\text{Vértice 3}=\left(\frac 32,-\frac 16+\frac 23 \right)=\left(\frac 32,\frac 12 \right)\\&\\&\text{Vértice 3}=\left(\frac 32,-\frac 16-\frac 23 \right)=\left(\frac 32,-\frac 56 \right)\\&\\&\text{La semidistancia focal es}\\&\\&c= \sqrt{a^2-b^2}=\sqrt{\frac {12}9-\frac 49}=\frac{2 \sqrt 2}{3}\\&\\&\text{Los focos son}\\&\\&Foco\;1=\left(\frac 32+\frac{2 \sqrt 2}{3},-\frac 16 \right)=\left(\frac{9+4 \sqrt 2}{6},-\frac 16 \right)\\&\\&Foco\;1=\left(\frac 32-\frac{2 \sqrt 2}{3},-\frac 16 \right)=\left(\frac{9-4 \sqrt 2}{6},-\frac 16 \right)\\&\\&\\&\end{align}$$Y esta es la imagen con los puntos introducidos con la misma expresión que se obtuvo para comprbar que están bien
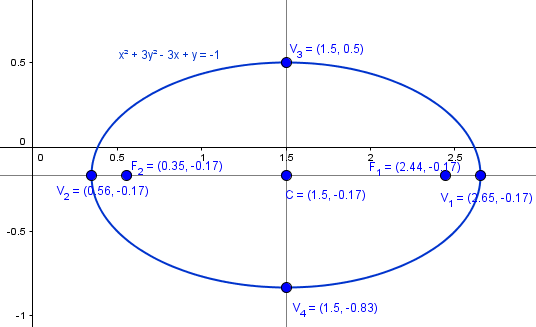
Luego está bien.
Y ya está. Si quieres el que queda debe ir en otra pregunta.
Saludos.
:
:
Después de todo lo que he trabajado, como vea algún punto para Herrera por esa estupidez que ha contestado, se acabó contestar preguntas tuyas.
¡Gracias!
Mat, si crees que Jorge Herrera se merece algúbn punto por eso que escribió lo siento pero dejarás de contar con mis respuestas, quédate con las suyas si te agrada, Hombre es gordo que todo lo que he trabajado me lleve 300 puntos y el que no no ha hecho nado ase lleve 200. Suopongo que entenderás perfectamente mi actitud y no tenrás más respuestas mías mientras no le quites esos puntos que no se merece de ninguna forma. Es que incluso le has dado lo mismo que a Gustavo que ha trabajado. Vergonzoso.
Intentaré resolver el ejercicio b)
( @Jorge Herrera, te agradecería no me uses en tu guerra personal ya que, por otra parte, estoy del lado de Valero Angel Serrano Mercadal pues lo único que estás haciendo es copiar/pegar link, o incluso ahora ni siquiera eso -te anticipo que el voto negativo que tienes es mío)
$$\begin{align}&x^2-y^2+x+y-1=0\\&\text{Completemos cuadrados}\\&(x+\frac{1}{2})^2 - \frac{1}{4} - (y - \frac{1}{2})^2 + \frac{1}{4} - 1=0\\&(x+\frac{1}{2})^2 - (y - \frac{1}{2})^2 =1\\&\text{Es una hipérbola horizontal (x positivo), cuya expresión general es}\\&\frac{(x-m)^2}{a^2} - \frac{(y-n)^2}{b^2}=1\\&Centro: (-\frac{1}{2},\frac{1}{2})\end{align}$$Te dejo la imagen...
Salu 2
Voy a remitir tu pregunta al usuario Gustavo Omar Fellay quien gustosamente la responderá.