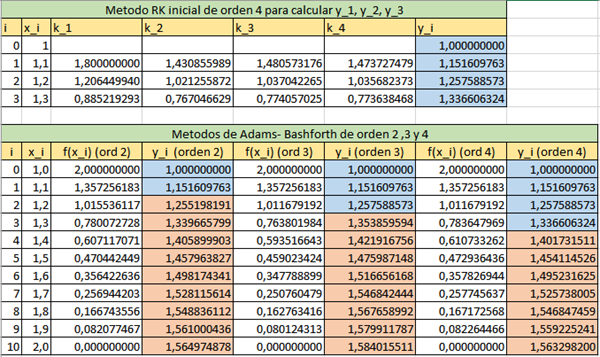
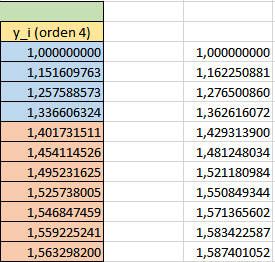
Hallar la solución aproximada que proporciona el Método de Adams – Bashforth de segundo, tercer y cuarto orden para la ecuación
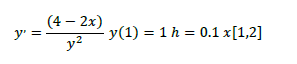
......,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,_____________________________________________________________________________-----------------------------------------------------------------ñ.............................
1 Respuesta
·
·
¡Hola Juan David!
Esto he encontrado sobre los métodos de Adams-Bashforth:
Como se puede ver, serán muchas cuentas, luego vamos a hacer una hoja de Excel que las haga.
Para poder tener valores y_0 y y_1 en el método de orden 2, y tener también y_2 en el método de orden 3 y también y_3 en el método de orden 4, se usará primero un método de Runge-Kuta de orden 4.
Y esta es la hoja de Excel.
Y esta es hoja de claculo para que veas las fórmulas y corrijas algo si me equivoqué
https://drive.google.com/file/d/0B3nG6r7qbZZ_RUU5U0RpUkhISkU/view?usp=sharing
···
Y ya solo quedaría comprobar si esta bien. Sería terrible si no, de todas formas yo mando lo que he hecho que menudo trabajo me ha costado.
Aunque es una ecuación de variables separables ya estoy tan agotado que me la resolverá WolframAlpha, la solución es
$$\begin{align}&y= \sqrt[3]{-3x^2+12x-8}\end{align}$$La cual evaluada en esos puntos nos da
Y no parece que vayan muy desencaminados, luego díria que está bien.
Y eso es todo, sa lu dos.
:
.
