Resolver las siguientes problemas en hallar el calculo

·

·

¡Hola Andrés!

El llamado 15 es todo un señor ejercicio por sí mismo, de lo más complicado que se puede poner en volúmenes de revolución.

Este es un dibujo de un ejercicio parecido donde sale la misma función:

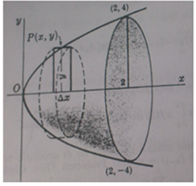
Al desplazar el eje Y a la recta x=2 la función queda

y^2 = 8(x+2)

Ya que para el nuevo x= 0 el valor de y será el del antiguo x=2

despejamos x 

x = y^2 / 8 - 2

Los puntos y de corte con el nuevo eje Y son

0 = y^2 / 8 - 2

y^2 /8 = 2

y^2 = 16

y= -4 y 4

Y la fórmula del volumen girando alrededor del eje Y es:

$$\begin{align}&V=\pi \int_{y_1}^{y_2}f(y)^2dy\\&\\&V=\pi\int_{-4}^4 \left(\frac{y^2}{8}-2  \right)^2dy=\\&\\&\text{Como vemos que es simétrica respecto al eje x}\\&\\&2\pi\int_0^4 \left(\frac{y^2}{8}-2  \right)^2dy=\\&\\&2\pi\int\left(\frac{y^4}{64}-\frac {y^2}2+4  \right)dy=\\&\\&2\pi\left[\frac {y^5}{5·64} -\frac{y^3}6+4y \right]_0^4=\\&\\&2\pi\left(\frac{1024}{5·64}-\frac{64}{6}+16  \right)=\\&\\&2\pi \left(\frac {16}5-\frac{32}{3}+16  \right)=\\&\\&2\pi\left(\frac {48-160+240}{15}  \right)= 2·\frac {128}{15}\pi=\frac {256}{15}\pi u^3\end{align}$$

Luego la respuesta es la b)

Lo siento, cada una de estas preguntas es un ejercicio más que aceptable, tendrán que ir uno en cada pregunta.

Sa lu dos.

:

: