Dibuje la region limitada por las graficas de las funciones algebraicas y calcule el area de la region.
En los siguientes ejercicios dibuje la region limitada por las graficas de las funciones algebraicas y calcule el area de la region.
Describa el metodo empleado para calcular el area de entre las dos funciones.
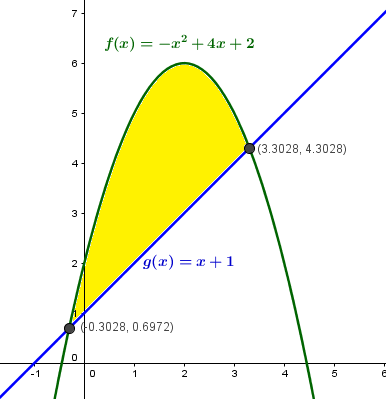
Ejercicio 1.
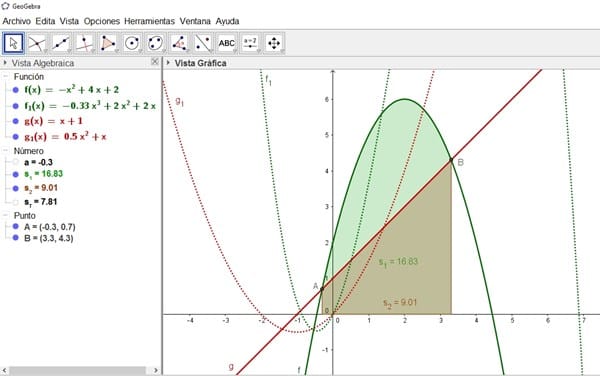
$$\begin{align}& f(x)=-x^2+4x+2,g(x)=x+1\end{align}$$Ejercicio 2
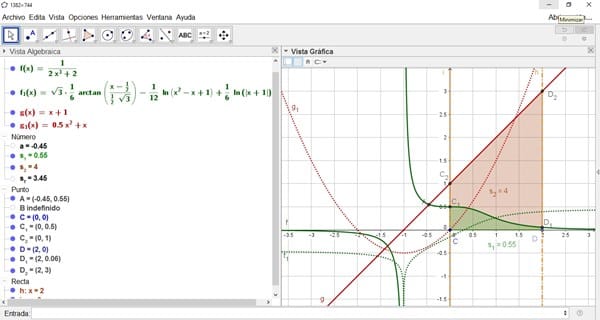
$$\begin{align}& y=1/2 x^3+2,y=x+1,x=0,x=2\\&\end{align}$$
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta de Enrique Ezpeleta
1