Anónimo
Cálculos relacionados con el movimiento circular Definición de movimiento circular uniforme y no uniforme,Periodo,Frecuencia
¿Qué producto entregarás?
Un documento donde presentes el procedimiento y la respuesta a los cuatro cálculos solicitados: frecuencia, periodo, velocidad angular de la rueda (en rad/seg) y velocidad tangencia.
¿Qué hacer?
1. Extrae los datos del siguiente enunciado para resolver los cálculos solicitados.
Una rueda de bicicleta tiene un radio de 50 cm y gira a razón de 120 vueltas por minuto.
2. Soluciona lo que se te pide:
a) Primero, calcula la frecuencia. Recuerda que la frecuencia es el número de vueltas por segundo, entonces hay que pasar de minutos a segundos (1min = 60 segundos). Su fórmula es:
b) Posteriormente, obtén el periodo, que es el tiempo que tarda una vuelta y es inverso a la frecuencia. Su fórmula es:
c) Ahora, calcula la velocidad angular (w) con la fórmula donde incluyas los valores anteriores:
Nota: Recuerda que deberás convertir los rev/min a rad/seg donde 1 rev = 2π rad y 1 min = 60 seg.
d) Por último y a partir del resultado obtenido en el punto 3, encuentra la velocidad tangencial, cuya fórmula es:
3. Integra en un documento los cuatro incisos con sus respectivas respuestas, incluyendo el proceso que seguiste para obtener el resultado y súbelo a la plataforma con el siguiente nombre:
Apellidos_Nombre_M19 S3 AI5 Cálculos que involucran movimiento circular
1 respuesta
·
·
¡Hola Felipe de Jesús!
2a) La frecuencia es el número de ciclos entre el número de segundos.
Tenemos 120 ciclos en 1 minuto = 60 segundos
f = 120 / 60 s = 2 s^(-1) = 2 Hz
·
2b) El periodo es el inverso de la frecuencia
T = 1/f = 1/[2 s^(-1)] = 0.5 s
·
2c) Nos dan dos formas de calcularla
$$\begin{align}&w= \frac{2\pi}{T}= \frac {2\pi}{0.5 s}= 4\pi\,s^{-1}\\&\\&w= 2\pi·f = 2\pi·2s^{-1}= 4\pi \,s^{-1}\\&\\&\\&d) \text{ Hay que pasar el radio a metros}\\&\\&r=50cm=0.5m\\&\\&v=wr= 4\pi\,s^{-1}·0.5m = 2\pi\, m/s\end{align}$$Y eso es todo, saludos.
:
:
Bueno 2c) está mal, pero es porque las fórmulas que han puesto también están mal. No hay que omitir el rad en las fórmulas y luego sacárselo de la chistera. Que molesta, ya sé que molesta, pero tiene que estar en las fórmulas para que las medidas se puedan deducir correctamente.
$$\begin{align}&w= \frac{2\pi\,rad}{T}= \frac {2\pi\,rad }{0.5 s}= 4\pi\,rad/s\\&\\&w= 2\pi\,rad·f = 2\pi\,rad ·2s^{-1}= 4\pi \,rad/s\\&\\&\\&d) \text{ Hay que pasar el radio a metros}\\&\\&r=50cm=0.5m\\&\\&v=\frac{wr}{rad}= \frac{4\pi\,rad/s·0.5m }{rad}= 2\pi\, m/s\end{align}$$
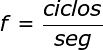
Buenos días, está resolviendo un problema de calentador, no de bicicleta, gracias. - Gaby Montes
No te metas donde no te llaman gaby michel , estamos en el modulo 19 en la actividad CÁLCULOS RELACIONADOS CON EL MOVIMIENTO CIRCULAR , somos la primera generación, el modulo y actividad del calentador ya es pasada para nosotros. - Anónimo
Ademas estas con el Profesor Valero, un GENIO y un gran Maestro y amigo. Gracias Profesor Valero por su paciencia. - Mayrena Espinosa
Sres. Felipe de Jesus Y Mayrena Espinosa, supongo que tienen educación como para corregir a alguien, realmente, estaba el respetado y genio Profesor Valero, unn problema de calentador que por error estaba mal, y no por su culpa, al profesor, jamás lo cuestioné y demuestren su educación, de que les sirve estar em la !a generación, si son unos majaderos, no entendieron el tema de la nética, ya que no saben comportarse en red. Muchas gracias por su atención y si siguen con sus groserías, puedo reportarlos a prepa en línea, como plagiarios de un trabajo que realiza un profesional. Disculpe Ud. Profesor Valero, es que hay que educar a estos ciudadanos!!! - Gaby Montes
Netiqueta! y sin comentarios... - Mayrena Espinosa
Acepto el error, por lo menos aprendiste algo Mireya y sabes, es foro para aprender no para discutir, gracias por la corrección, y sí, sabes leer, pero no entender. Fin de mi comentario a tú persona!!! - Gaby Montes
Mayrena! ¿? ... - Mayrena Espinosa
Valero, gracias por compartir de su sabiduría, con sencillez y destreza. La más de las veces me hace falta este tipo de pasos cuando me siento frente a una hoja en blanco. Saludos - Polibio De Arcadia