Lee y analiza el planteamiento. Analiza el siguiente problema.
Elaborar una presentación con diapositivas donde respondas a los planteamientos realizados: la gráfica de la función principal, tu respuesta a las preguntas del punto dos, las gráficas que representan la recolección de tapas y la ecuación de la recta secante con su pendiente, con tu explicación en un audio.
Una asociación contra el cáncer de niños se encarga de recolectar tapas de refrescos desechables con el propósito de venderlas y así obtener una cantidad de dinero extra para continuar con su labor.
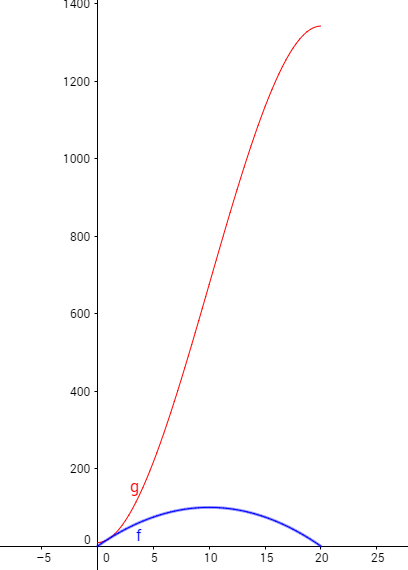
Según su estadística, la ecuación que representa el número de tapas a recolectar es la siguiente f(x)= -x2 + 20x donde señala la cantidad de tapas recolectadas. Ligado a esto, la asociación ya cuenta con 9,000 tapas que ha recolectado por su cuenta.
2. Realiza el bosquejo de la gráfica que representa la ecuación y con ayuda de la gráfica responde las siguientes preguntas:
a) ¿Cuál es el punto máximo del número de tapas que se recolectan, así como el tiempo en el que ya no se recolecta nada? (No olvides que los resultados son en miles).
b) ¿Cuál es la relación que existe entre el tiempo y el número de tapas que se juntaron? Y ¿Cuál sería el total de tapas en punto máximo en conjunto con lo ya obtenido por la asociación con anterioridad?
Nota: Para incluir la gráfica en tu presentación puedes usar la cámara de tu celular y tomar una fotografía. Es importante que recuerdes que la gráfica debe ser elaborada a mano mediante el proceso revisado en el tema de “Funciones” de la semana 1.
3. Obtén la ecuación de la recta secante a partir de la función derivada (de la que ya te fue dada anteriormente) y el valor de su pendiente. Luego, intégrala en la misma gráfica anterior y responde (en un audio) a la siguiente pregunta:
c) Qué relación existe entre el punto máximo alcanzado y la recta secante y su pendiente; relaciónalo con los datos obtenidos en tu actividad.
Considera que para la pendiente tendrás que usar los siguientes valores:
X1 = 9,000(tapas ya recolectadas)
Y2 = el punto máximo obtenido de tu gráfica
2 respuestas
Cobali, si lees con atención la respuesta dada por el profe Valero Angel Serrano Mercadal, verás que aplican las mismas consideraciones excepto en el punto 2b)
Sabemos que la función que representa la cantidad de tapas acumuladas, será la integral de f(x), y para mantener la relación con la respuesta del profe, la voy a llamar g(x)
Sabemos que
$$\begin{align}&g(x) = -\frac{x^3}{3} + 10x^2+C\\&\text{Calculamos C, para que g(0) = 9 (este es el único cambio entre ambas preguntas)}\\&g(0) = 9 = -\frac{0^3}{3} + 10\cdot 0^2+C \to C = 9\\&\therefore g(x) = -\frac{x^3}{3} + 10x^2+9\end{align}$$Si bien no lo pide te voy a agregar algo más, ya que el profe ya resolvió todo (por esto te pido que votes tanto allá como acá la respuesta)
Como ves la función g(x) es una cúbica con coeficiente negativo, por lo que llegará un punto en que esa función llegará a su máximo (local) y a partir de ahí empiece a decrecer, cosa que en realidad no tiene sentido ya que cada vez acumulas más tapas y no menos.
Puedes derivar para ver cual ese ese 'máximo' pero como ya el profe nos calculó todo, tenemos que ese valor es 20 (que es la zona de validez de f(x))
Por lo tanto la función g(x) está solo definida para x entre 0 y 20 y tendría esta forma:
Te dejo ambas funciones (f: recolección diaria, g:acumulada) en un solo gráfico
Salu2 y no olvides valorar ambas respuestas
Respecto a los comentarios, lo que cambia entre la respuesta con 60000 tapas y con 9000 es la constante de integración de la función g(x) = 'Cantidad de tapas acumuladas'
Como bien dicen también faltó la cantidad de tapas acumuladas y eso es g(x) para el último día, o sea g(20)
$$\begin{align}&g(20) = - \frac{20^3}{3} + 10\cdot 20^2 + 9= 1342.33\end{align}$$Salu2
Ayuda por favooor!
El maestro valero da la respuesta con 60000 tapas y ahora es con 9000 y la que interesa es la de 9000 gracias - Ricardo Ramirez
Gracias por la ayuda - Ricardo Ramirez
Sabe maestro le falto cual fue el total de tapas recolectadas - Ricardo Ramirez
Entonces sabrán como queda con el ejercicio de 9000 tapas - Ivan Thomas