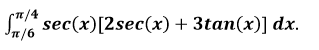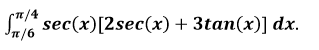La integración temáticas de la integral indefinida, la integral definida y los teoremas

;)
Hola Carolina Menjura!

$$\begin{align}&\int_ \frac{\pi} 6^{\frac {\pi} 4} 2 sec^2x dx= 2 tan(x) \Bigg |_ \frac{\pi} 6^\frac {\pi} 4=2 \Big(1 -\frac {\sqrt 3} 3 \Big)=2-  2 \frac{\sqrt 3} 3\\&\\&\int_ \frac{\pi} 6^{\frac {\pi} 4} 3secx·tanx dx=3\int_ \frac{\pi} 6^{\frac {\pi} 4} \frac 1 {cosx}·\frac{senx}{cosx} dx=\\&\\&3\int_ \frac{\pi} 6^{\frac {\pi} 4} \frac{senx}{\cos^2x} dx=3\int_ \frac{\pi} 6^{\frac {\pi} 4}senx·\cos^{-2}(x )dx=3 \frac{\cos^{-1}x}{-1}(-1)\\&\\&\frac 3 {cosx} \Bigg|_{\frac{\pi} 6}^{\frac{\pi} 4}=3 \Big( \frac 2 {\sqrt 2}- \frac 2 { \sqrt 3} \Big)=\frac{6 \sqrt 3- 6 \sqrt 2}{\sqrt 6}=\\&\\&\frac{6 \sqrt {18}- 6 \sqrt {12}}{6}=\sqrt{18}- \sqrt{12}= 3 \sqrt 2 - 2 \sqrt 3\\&\\&\\&\int (2 sec^2xdx+3secxtanx)dx=2-  2 \frac{\sqrt 3} 3+3 \sqrt 2 - 2 \sqrt 3=2+ 3 \sqrt 2- \frac 8 3 \sqrt 3 \simeq1.62384\end{align}$$

Saludos

;)

;)