Como resolver con integrales y análisis de gráficas
Cada ejercicio se debe resolver paso por paso, sin omitir ninguno, cuando se utilice una propiedad, definición o ley por favor enunciarla, así se fortalece el procedimiento utilizado.
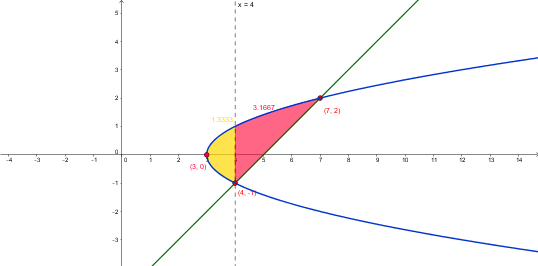
2. Encuentre el área de la región comprendida entre la parábola
$$\begin{align}&y2 =x-3\end{align}$$la recta
$$\begin{align}&y=x-5\end{align}$$Sugerencia: Elabore la gráfica para una mejor comprensión del ejercicio.
Respuesta de Lucas m
3
;)
Hola Laura!
Es una parábola horizontal, simétrica respecto el eje X
Calculemos su vértice, que es el punto de corte con el eje X:===> y=0
$$\begin{align}&0=x-3 ===> x=3\end{align}$$Buscamos el punto de corte entre las dos curvas:
$$\begin{align}&y^2=x-3\ ===> x=3+y^2\\&y=x-5 ====>x=5+y\\&\\&y^2+3=5+y\\&\\&y^2-y-2=0\\&\\&y_1=2 ===> x_1=7\\&y_2=-1 \ ===> x_2=4\\&Tenemos \ dos \ recintos:\\&\\&A_1=2 \int_3^4 \sqrt{x-3} dx= 2· \frac{(x-3)^\frac 3 2}{\frac 3 2}=\frac 4 3 (x-3)^\frac 3 2 \Bigg|_3^4=\\&\\&\frac 4 3 \Big(1-0\Big)= \frac 4 3 \ u^2\\&\\&A_2=\int_4^7 \Big( \sqrt {x-3}-(x-5) \Big) dx= \frac{(x-3)^\frac 3 2}{\frac 3 2 }- \frac{x^2}{2}+5x \Bigg|_4^7=\\&\\&\frac 2 3 {4^\frac 3 2}- \frac{49} 2+35- \Big( \frac 2 3·1-8+20 \Big)=\\&\\&\frac 2 3·8- \frac {49}2 +35- \frac 2 3+8-20= \frac{19} 6 \ u^2\\&\\&A_{total}=\frac 43 +\frac{19} 6 =\frac 9 2= 4.5 \ u^2\end{align}$$
Saludos
;)
;)
