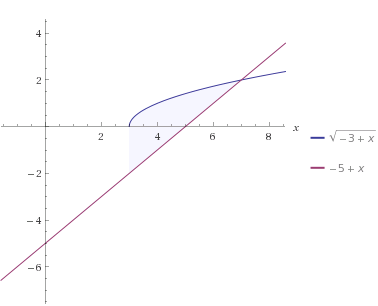
Encuentre el área de la región comprendida entre la parábola

Encontrar la parábola comprendida entre la siguiente integración.

Respuesta
1

;)
Hola Juan!
La contesté en el siguiente enlace: area parábola

Recuerda regresar aquí y votar a todos los expertos

Saludos

;)

;)

1 respuesta más de otro experto

Respuesta
1

Primero tienes que encontrar la intersección entre las dos curvas dato.

( x-5)^2 = x-3 ............la resolves y te esta dando x=7.

Por otro lado la parábola tiene por ordenada mínima x = 3 ( no esta definida para x<3 en campo real).

Area entre ambas = Integral ( f(x) - g(x)) dx entre X1= 3    Y   x2= 7

http://www4f.wolframalpha.com/Calculate/MSP/MSP38601c5bc424g4f47b9600001ih1094a1158dea4?MSPStoreType=image/gif&s=57&w=272.&h=37.

Te participo de lo que yo estaría integrando:porque veo que no habia salido nada antes:

Por eso pongo los limites entre 3 y 7. Me refiero al área sombreada.

La integral no es difícil y a mi me daba 5.333 unidades de superficie.

Añade tu respuesta

Haz clic para o

Más respuestas relacionadas

Qué puedo hacer con el frigorífico?

Tengo un combi de mínimo 10 años, no sé exactamente cuántos y hace unas semanas empezó a hacer un zumbido fuerte. Hoy lo he mirado x detrás y un cable está carbonizado y otro quemado. También el enchufe algo quemado. ¿Está para tirar? Incluyo enlace...
3 respuestas

Casquillos electrolíticos en deposito de inercia

He puesto un deposito de inercia de 200 litros para calentar agua mediante una resistencia de 3000w, ¿Le tengo que poner entre la resistencia y el deposito un casquillos electrolítico para evitar la corrosión del deposito? ¿Sería bueno también...
2 respuestas

ChatGPT Polsku: Innowacyjne Rozwiązania dla Każdego w 2024

ChatGPT Polsku, w najnowszej wersji na rok 2024, oferuje użytkownikom szeroki wachlarz unikalnych funkcji, które sprawiają, że jest to niezastąpione narzędzie w codziennym życiu. Jedną z kluczowych cech, która wyróżnia tę platformę, jest jej...
14 respuestas

Software en ing. Industrial

Deseo saber cuales son las herramientas, programas o software que debe tener todo ing. Industrial a la mano para su trabajo. Ejemplo. Productividad, procesos, proyectos, planta, mercadeo.
2 respuestas

¿Cómo elegir una calculadora estadística para trabajar con probabilidades?

Necesito encontrar una calculadora estadística para trabajar con probabilidades, pero aún no puedo decidir cuál es la mejor. ¿Qué funciones y características debería tener una calculadora de este tipo para poder realizar las tareas con eficacia?
3 respuestas

Catia v5 como hacer un perfil externo a una figura

Tengo una figura en 3d y necesito hacer un contorno, pero que este separado de esa figura un par de milímetros, y que ese contorno tenga una altura de unos 2 cm
1 respuesta

Consumo aerotermia vs aire acondicionado

Deseo cambiar la caldera de gasoil de mi vivienda (150 M2 aprox y divididos en dos plantas). Me aconsejan aire acondicionado (inverter con bomba de calor) o aerotermia de alta temperatura. ¿Cuál es mejor y cuál consume menos? ¿Cómo puedo calcularlo?...
4 respuestas

Motor de cortadora de pasto eléctrica se apago!

Estaba usando la cortadora de pasto sin problemas y sin causarle esfuerzo al motor ya que solo estaba retocando el jardín, y de la nada el motor se apaga... Revise las conexiones del interruptor, que no hubiera saltado ninguna térmica ni nada, la...
1 respuesta

Puedo cambiar la pieza de Unión de la resistencia del termofón por una de plástico ?

Saltó la llave del termofón y tuve que mirar la resistencia, sin saber qué hacer a priori pensé que la resistencia estaba quemada y sabía que el dado de conexión de la resistencia Luego vi que la resistencia estaba bien quise volver a meter la pieza...
3 respuestas

Filtro de aire toyota proace

Tengo un toyota proace city family de gasolina 110 cv. Quiero cambiarle el filtro y sé como hacerlo, pero el modelo de filtro viene en un kit con el filtro una espumita cuadrada que o sé dónde poner. ¿Puedes decirme dónde ponerla y si sabes cómo...
2 respuestas