Quien sabe de física general
Una partícula que describe una trayectoria en línea recta hacia la derecha, está condiciona a moverse según la ecuación x(t)=D1 m+(D2 m/s)t-(D3 m/s2)t2, donde “x” representa la posición de la partícula en metros y “t” el tiempo en segundos.
A. Determine la velocidad inicial, posición inicial y aceleración inicial de la partícula (Esto es para t=0 s). B. ¿En qué instante “t” la partícula tiene velocidad cero?
C. ¿Cuánto tiempo después de ponerse en marcha regresa la partícula al punto de partida?
D. ¿En qué instantes t la partícula está a una distancia de x1 m de su punto de partida?
E. ¿Qué velocidad (magnitud y dirección) tiene la partícula en cada uno de esos instantes?
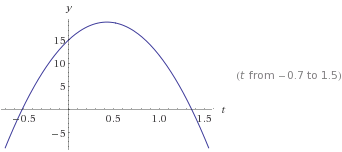
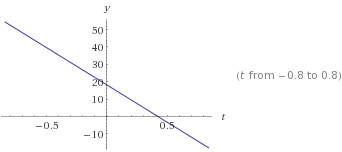
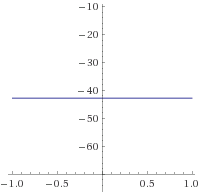
F. Dibuje las gráficas: x-t, Vx-t y ax-t para el intervalo de t = 0.0 s a t = t1 s.
NOTA: Para las gráficas utilice un programa graficador como lo puede ser GEOGEBRA. * Recuerde, los valores de D1, D2, D3, x1 y t1 los encuentran en la tabla de datos. Son 5 ejercicios en total, uno para cada integrante del grupo.
Datos:
d1:15.0
d2:18.1
d3:21.4
x1:4.00
t1:4.00
1 Respuesta
Tu ecuación de trayectoria seria:
-21.4 t^2 + 18.1 t + 15 = x(t)
x'(t)= velocidad(t) = - 42.8 t + 18.1
x''(t) = -42.8
A) Posicion inicial = 15 metros..........Velocidad inicial= 18.1 m/s ............Acel. inicial= -42.8 m/s^2
B) La particula tendra velocidad 0 para t= 18.1 / 42.8 = 0.423 s.
C) EL tiempo de regreso al punto de partida = tiempo en que anulo la velocidad o sea:
Tiempo de regreso = 2 x 0.423 = 0.845 s.
D) Se ubica a 4 metros del punto de partida para los tiempos:
19m = -21.4 t^2 + 18.1 t +15 ...................Siendo
∆ = (18.1)2 - 4·(-21.4)·(-4) = -14.79 la partícula nunca llegara a alejarse 4 metros hacia la derecha de la partida.
Cuando vuelve estará a 4 metros para el tiempo t1 que llegue ( hacia la izquierda) a 15-4 = 11 metros.
11= -21.4 t1^2 + 18.1 t1 + 15 ..........................t1 = 1.027 seg. ( la otra solucion se descarta por ser negativa).
E) Velocidad de la particula para t1 = 1.027 seg.......................
v( 1.027) = - 42.8 ( 1.027) + 18.1 = - 25.85 m/seg. ( direccion hacia la izquierda).
No me manejo con GEOGEBRA. Utilice WolframAlpha.
Trayectoria.x(t) en metros..para t>0.
Velocidad (t)......eje y representaria velocidad en m/s....... t>0.
Aceleracion(t)= -42.8 m/s^2 constante.....t>0.
