Dos pequeños discos deslizan sin fricción sobre una mesa horizontal
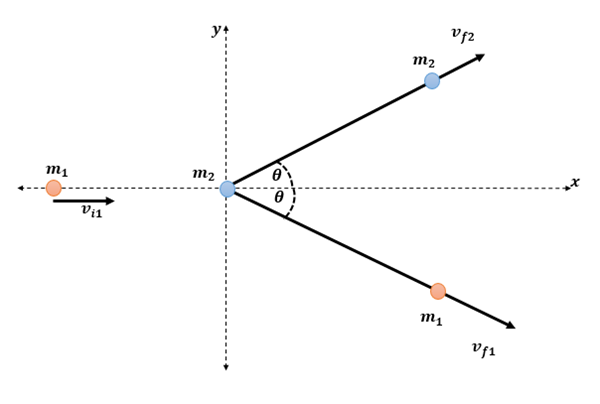
Dos pequeños discos deslizan sin fricción sobre una mesa horizontal. El primer disco, de masa m1, es lanzado con rapidez vi1 hacia el segundo disco, de masa m2, que inicialmente está en reposo.
Después de la colisión, ambos discos adquieren velocidades que están dirigidas a θ grados a cada lado de la línea original de movimiento del primer disco (ver figura ).
(a) ¿Cuáles son las rapideces finales de los dos objetos? (
$$\begin{align}&(Vf1 Y Vf2)\end{align}$$(b) ¿Es la colisión elástica o inelástica?
DATOS
m1 (kg)4,60
Vi1 (m/s)5,00
m2 (kg)2,50
θ (Grados)31,9
Ayuda con procedimientoy solucion Gracias
...
...
...
...
1 Respuesta
Es una colisión elastica y el desarrollo te lleva bastantes cálculos.
Partís de las dos ecuaciones fundamentales: Conservación de la cantidad de movimiento del sistema y Conservación de la Energía cinética del sistema.
Conservacion de la cantidad de movimiento: vi2=0
m1 vi1 =(componente solo en i) = 4.60 x 5 = 23 = 4.60 .( cos 328.1)( vf1) + 2.50( cos 31.9) ( vf2)
luego de hacer las cuentas llegas a:
3.90 vf1 + 2.122 vf2 = 23 ....(1)
Conservacion de la Energia cinetica:
4.60 vf1^2 + 2.50 vf2^2 = 4.60 x 25 = 115 ....................(2)
De la (1) despejas... vf1^2 = (23 - 2.122 vf2)^2 / 3.90^2... haces el desarrollo y llegas a:
Vf1^2 = 34.78 - 6.41 vf2 + 0.296 vf2^2
Si llevas esto a la (2) y desarrollas toda la expresion tendrias al final:
160 - 29.5 vf2 + 3.83 vf2^2 = 115
3.83 vf2^2 - 29.5 vf2 + 45 = 0
Resolves la cuadratica y llegas a la solucion vf2 = 2.1 m/s
vf1 = (23 - 2.122 x 2.1) / 3.90 = 18.54 / 3.90 = 4.75 m/s.
Revisa bien los cálculos... por ahí se me colo algún error.
Gracias Sofia.
