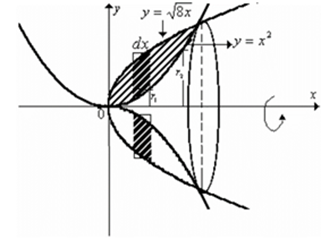
Hallar el volumen del solido que se genera al girar la región plana R:{(y=x^2 y= √8x) alrededor del eje x (ver figura).
Me pueden ayudar con este ejercicio
Hallar el volumen del solido que se genera al girar la región plana R:{(y=x^2 y= √8x) alrededor del eje x (ver figura). El volumen se expresa en unidades cúbicas.
1 respuesta
Respuesta de Lucas m
1
;)
Hola jennifer!
Se calcula con la fórmula:
$$\begin{align}&V= \pi \int_a^b\Big( f(x)-g(x)\Big)^2 dx=\\&\\&Buscamos\ los \ puntos \ de \ corte\ de \ las \ funciones\ igualando:\\&\\&y=x^2\\&y= \sqrt 8 x\\&x^2=\sqrt 8 \ x\\&\\&x^2- \sqrt 8 \ x=0\\&\\&x(x- \sqrt 8)=0\\&\\&x_1=0\\&x_2= \sqrt 8\\&\\&V= \pi \int_0^{\sqrt 8} \Big(8x^2-x^4 \Big) dx= \pi \Bigg[ \frac {8x^3}3- \frac {x^5} 5 \Bigg]_0^{\sqrt 8}=\\&\\&\pi \Bigg( \frac { 8 \sqrt 8^3} 3- \frac { \sqrt 8^5}5 \Bigg)=\pi \Bigg( \frac {64}3 \sqrt 8- \frac {64} 5 \sqrt 8 \Bigg)=\\&\\&\pi \sqrt 8 \frac {128}{15}\ \ u^3=75.825\ \ u^3\end{align}$$Saludos
;)
;)
La fórmula te la escribí mal, es:
$$\begin{align}&V= \pi \int_a^b \Big [f(x)^2-g(x)^2 \Big]dx\end{align}$$pero todo lo hecho es correcto.
;)
;)
