Problema sobre la potencia mecánica de un camión en un plano inclinado

Para resolver esto, debes tener claro el caso en el que nos encontramos. Tenemos un plano inclinado en 15º y un camión que sube a velocidad constante, por lo que la aceleración que tendrá será 0. Como no se considera la fricción solo nos interesaran las componentes de la fuerza en la dirección del mismo plano inclinado. En el dibujo siguiente se representa suficientemente bien.

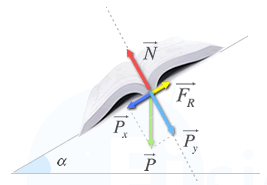
Si te fijas bien, el angulo alfa es el que hay entre el peso P y el peso en la dirección y (Py). La Fr no existe, pero si que tenemos la fuerza que hace el motor del camión que va en esa dirección. Por lo tanto, el sumatorio de fuerzas nos queda como:

$$\begin{align}&\sum\vec{F}=m·\vec{a}\end{align}$$

Como sube a velocidad constante la aceleracion es 0 y nos queda:

$$\begin{align}&\sum\vec{F}=0\\&P_x-F=0\\&P_x=F\end{align}$$

Ahora, el Px es, por relaciones trigonometricas, el seno del angulo alfa multiplicado por P.

$$\begin{align}&P·\sin(\alpha)=F\end{align}$$

El peso de un objeto se define como el producto de su masa por la gravedad

$$\begin{align}&m·g·\sin(\alpha)=F\end{align}$$

Lo unico que falta recordar es que la potencia es la fuerza por la velocidad, así que finalmente nos queda algo como:

$$\begin{align}&Pot=v·m·g·\sin(\alpha)\end{align}$$

Sustituimos en la ecuacion por nuestros valores y tenemos que la potencia que necesita el camion es de:

$$\begin{align}&Pot=15m/s·50.000kg·9.81m/s^2·\sin(15º)=1.904.261W=1904 kW\end{align}$$

Espero haberte ayudado. Si tienes alguna duda no dudes en preguntarme. Salu2.