Como desarrollo este ejercicio para calcular las Áreas

Lo primero que tenés que hacer acá es la gráfica de lo que te piden, para entender justamente que necesitas...

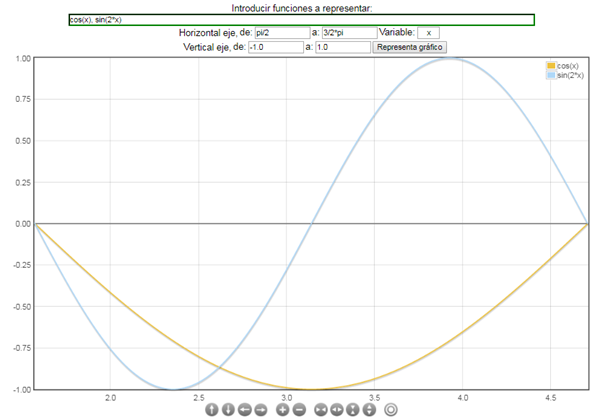
Vemos que en una primera parte, la función coseno está por arriba del seno, y a partir de un punto, esto queda al revés... lo importante es encontrar ese punto, para eso, hacemos

cos(x) = sen(2x)

Haciendo los cálculos, llegás a que ese valor donde ambas funciones son iguales es 5/6 PI, por lo tanto el área en cuestión queda:

$$\begin{align}&Area = \int_{\pi/2}^{5/6 \pi} \cos(x) - sen(2x) dx + \int_{5/6 \pi}^{3/2 \pi} sen(2x) - \cos(x) dx=\\&\bigg( sen(x) + \frac{1}{2}\cos(2x)\bigg|_{\pi/2}^{5/6 \pi}\bigg) + \bigg(-\frac{1}{2}\cos(2x) - sen(x)\bigg|_{5/6 \pi}^{3/2 \pi} \bigg)=\\&\bigg( sen(\frac{5 \pi}{6}) + \frac{1}{2}\cos(\frac{5 \pi}{3})\bigg)-\bigg(sen(\frac{\pi}{2}) + \frac{1}{2}\cos( \pi)\bigg) + \bigg(-\frac{1}{2}\cos(3 \pi) - sen(\frac{3 \pi}{2})\bigg)-\bigg(-\frac{1}{2}\cos(\frac{5 \pi}{3}) - sen(\frac{5 \pi}{6})\bigg)=\\&sen(\frac{5 \pi}{6}) + \frac{1}{2}\cos(\frac{5 \pi}{3})-sen(\frac{\pi}{2}) - \frac{1}{2}\cos( \pi)-\frac{1}{2}\cos(3 \pi) - sen(\frac{3 \pi}{2})+\frac{1}{2}\cos(\frac{5 \pi}{3}) + sen(\frac{5 \pi}{6})=\\&2sen(\frac{5 \pi}{6}) + \cos(\frac{5 \pi}{3})-1 + \frac{1}{2}+\frac{1}{2} + 1=\\&1 + 0.5+ 1=2.5\end{align}$$

Notas:

1. Revisá las cuentas porque con tantos números, puedo haber errado alguno

2. Para hallar cos(x) = sen(2x) usé el método de Newton-Raphson, no se que tanto conocés los métodos de solución iterativos.

Salu2