Tema parábola ; ¿Como se podría resolver este ejercicio?
Sea la parábola y=-x²+4x+3. Hallar el área del triangulo limitado por la recta y=2; la tangente y normal a la parábola en el punto de abscisas 3
2 respuestas
El dibujo de los datos es
Supongo que se refieren al triángulo que queda comprendido por los vértices (0,12), (0,2), (5,2); pero no está aclarado que el otro límite del triángulo sea el eje Y
Asumiendo que esto es correcto, entonces vemos que quedó un triángulo rectángulo cuya base es 5 y altura 10, por lo que el área es de 25
Salu2
E.g.:
Diagrama geométrico que, lamentablemente, también contiene la solución, y que pido ignoréis mientras lo resolvemos por método algebráico y no geométrico:
La línea de color lila es la parábola (f(x)=
$$\begin{align}&-x^2+4x+3\end{align}$$)
.La recta verde es y=2.
La recta roja es la tangente a la parábola en el punto de abscisa 3. La ordenada del punto de tangencia (circulo negro) es (
La pendiente de la tangente coincide con la derivada de la parábola (-2x+4) en el punto de tangencia, i.e. -2. La ordenada
Perdón por el envío precoz. Empiezo de nuevo:
E.g.:
Diagrama geométrico que, lamentablemente, también contiene la solución, y que pido ignoréis mientras lo resolvemos por método algebráico y no geométrico:
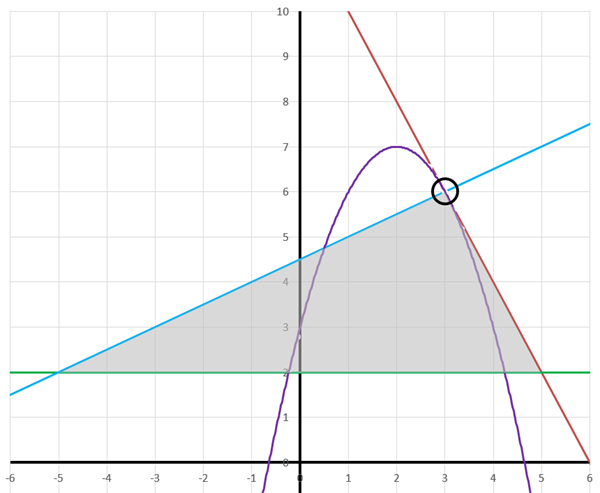
La línea de color lila es la parábola (f(x)=-x*x+4x+3). La recta verde es y=2.
La recta roja es la tangente a la parábola en el punto de abcisa 3. La ordenada en el punto de tangencia (circulo negro) es f(3)=..=6. Ese es el rpimer punto del triángulo: (3,6)
La pendiente de la tangente la podemos calcular usando la primera derivada de la parábola (-2x+4) evaluada en x=3 resulta -2. Usando la representación punto-tangente, la recta roja es:
-2 = (y-6)/(x-3); -> y= -2x +12.
La recta azul es la normal; Su pendiente es -1/m donde m es la pendiente de la tangente, i.e.
Usando la representación punto pendiente para la recta azul: 1/2 = (y-6)/(x-3); -> y=4.5+x/2.
El triangulo buscado es el marcado en gris. Para calcular las abcisas de intersección de las líneas roja y azul con la verde debemos resolver en qué abcisa cada una de las rectas toma una ordenada igual a 2, i.e.
Para la tangente: 2=-2x+12 => x= 5; --> Segundo vértice del triángulo: (5,2)
Para la normal: 2=4.5+x/2 => x= -5 ; --> Tercer vértice del triángulo: (-5,2)
La altura del triángulo es 6-2 =4; Su base 5-(-5)=10; Su área pues 4*10/2 =20.