Problema ecuaciones diferenciales de primer orden
Tengo un problema necesito calcular cual es la solución general y solución particular, de la siguiente ecuación
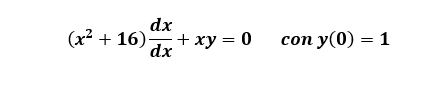
1 respuesta
Respuesta de Norberto Pesce
1

