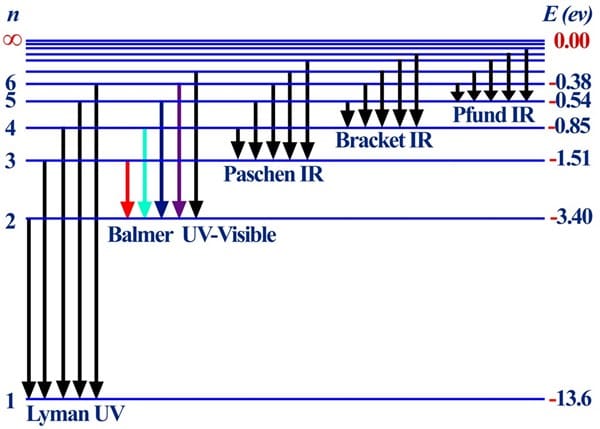
La línea de Balmer (espectro visible) tiene un nivel de llegada n=2, lo que me preguntan es de que nivel partió, como muestra la figura:
Si parte de n=3 emite un color rojo λ=656nm
Si parte de n=4 emite un color cian λ=486nm
Si parte de n=5 emite un color índigo o añil λ=434nm
Si parte de n=6 emite un color violeta λ=410nm
Si parte de n=7 emite radiación ultravioleta (sale del espectro visible) λ=397nm
bueno cada color tiene su longitud de onda λ, en nuestro caso λ=410nm que corresponde a la luz violeta o sea parte de n=6 y llega a n=2 Rpta n=6 PERO HAY QUE DEMOSTRARLO
ΔE = hC/λ ......(1) donde h=6.62x10^-34Jxs C=3x10^8m/s
E=-Eo/n^2........(2) donde Eo=2.18x10^-18J
λ=410x10^-9m en (1): ΔE = 6.62x10^-34x3x10^8/410x10^-9
ΔE = 4.8439x10^-19J que es la energía que se emite de ir del nivel "n"al nivel 2, aplicamos la ecuación (2):
ΔE = E(n) - E(2) = 4.8439x10^-19J
ΔE = - Eo/n^2 - (-Eo/2^2) = 4.8439x10^-19J
ΔE = - Eo/n^2 +Eo/4 = 4.8439x10^-19J
ΔE = +Eo(1/4 - 1/n^2) = 4.8439x10^-19
ΔE = (1/4 - 1/n^2) = 4.8439x10^-19 /Eo
1/n^2 =1/4 - 4.8439x10^-19 /Eo Eo=2.18x10^-18J
1/n^2 =1/4 - 4.8439x10^-19 /2.18x10^-18
1/n^2 = 0.25-0.2222 = 0.0278
n^2 = 1/0.0278 = 35.97 =36 entonces n = 6 lqqd (respuesta)

