Cómo resolver por método de integración por fracciones parciales
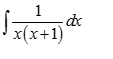
Buenas tardes, quien me puede colaborar con los pasos para resolver este ejercicio de Integrales.
Respuesta de Norberto Pesce
1

