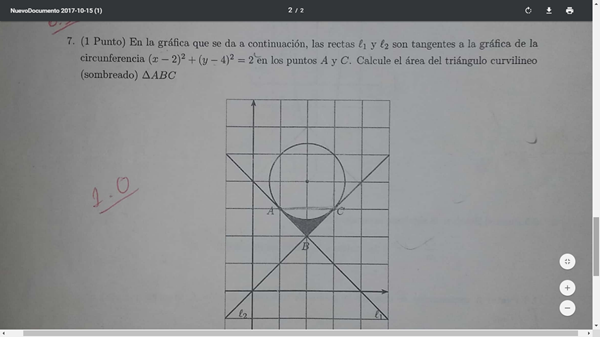
Ya tienes la respuesta como la pediste (mediante integrales). No se que tan estricto sea tu profesor, pero si yo veo ese ejercicio nunca se me hubiese ocurrido resolverlo mediante integrales, sino que lo haría directamente usando los conocimientos 'básicos' de geometría, ya que tenemos un círculo de diámetro 2 * raíz de 2 y un cuadrado de igual lado. Dicho esto vemos que el área buscada es un cuarto del área que queda entre la resta del área del cuadrado menos la del círculo. O sea
$$\begin{align}&\text{Area buscada: A}\\&A = \frac{1}{4} \bigg( A_{cuadrado}-A_{circulo} \bigg)\\&A = \frac{1}{4} \bigg( L^2- \pi r^2 \bigg)\\&A = \frac{1}{4} \bigg( (2 \sqrt{2})^2- \pi (\sqrt{2})^2 \bigg)\\&A = \frac{1}{4} \bigg( 8- 2 \pi \bigg)\\&A = \frac{1}{2} \bigg( 4- \pi \bigg) \approx \frac{0.85840734641021}{2} = 0.429203673205105\end{align}$$Que obviamente coincide con el valor que te dieron antes...
Salu2
Nota: entiendo que hay profesores que 'exigen' resolver los ejercicios por un método específico, si este es tu caso, entonces quedate con la solución anterior, aunque a mí me gusta pensar que si hay varias formas de resolverlos, cada uno debe buscar la suya (siempre y cuando los pasos sean correctos)


¿Cuándo lo leí, pensé exactamente lo mismo: Plantearlo por integrales?. Si la solución geométrica es para un niño de escuela primaria! - Boris Berkov