Encontrar la derivada direccional de las siguientes funciones en el punto dado y en dirección del vector v :
Derivada direccional
Encontrar la derivada direccional de las siguientes funciones en el punto dado y en dirección del vector v:
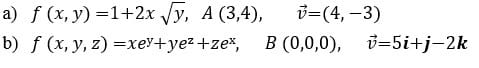
1 respuesta
Respuesta de Norberto Pesce
1

