Hallar el volumen del solido limitado por z=x^2+y^2, y=x^2, y=1, z=0

;)

Hola Oscar!

Si está bien escrito, ese y=1, complica bastante el asunto ya que la única zona cerrada que detecto es la que en la proyección en el plano XY te he dibujado en amarillo

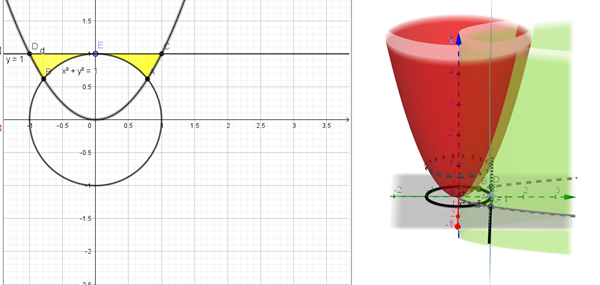
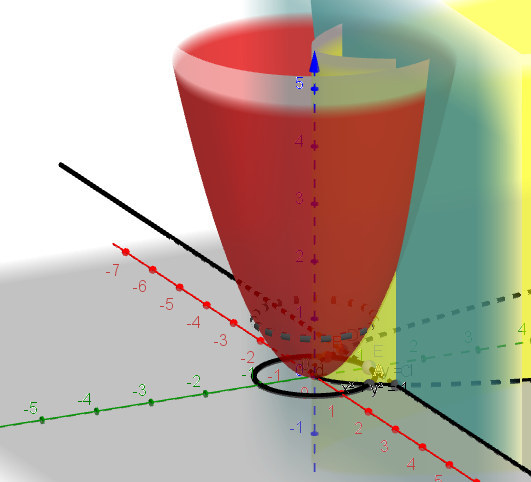
O sea que el volumen sería de esa región inferior, amarilla

Son dos zonas iguales, que a su vez se tendrían que descomponer en dos integrales triples:

Primero hemos de calcular el punto A, intersección entre la parábola y la circunferencia:

$$\begin{align}&y=x^2\\&x^2+y^2=1\\&\\&x^2+x^4=1\\&x^4+x^2-1=0\\&Bicuadrada:\\&x^2=t\\&\\&La \ solución º positiva \ es\\&t= \frac{-1+ \sqrt 5} 2=> x= \sqrt t=0.78615\\&Proyectando\ en \ el \ plano \ XY:\\&\\&R_1=\int_0^{0.78615} \ \int_{\sqrt{1-x^2}}^1 \int_{0}^{x^2+y^2}dz\ dy \ dx\\&\\&R_2= \int_{0.78615} ^1 \ \int_{x^2}^1 \ \int_0^{x^2+y^2} dz \  dy \ dx\end{align}$$

Saludos

;)

;)