Ecuaciones e intersecciones de rectas en la circunferencia
1: Determinar los puntos de intersección de las circunferencias; graficar
x^2+y^2=25 y x^2+y^2+x+y-20=0
2: Encuentre la ecuación de la recta que pasa por los puntos de intersección de las circunferencias; graficar.
x^2+y^2-6x-2y-6=0 ; x^2+y^2-12x+4y+31=0
1 Respuesta
Respuesta
2
Te dejo el primero...
En general siempre que puedas, te conviene empezar por el gráfico, ya que pueden darte información útil a la hora de resolver el ejercicio...
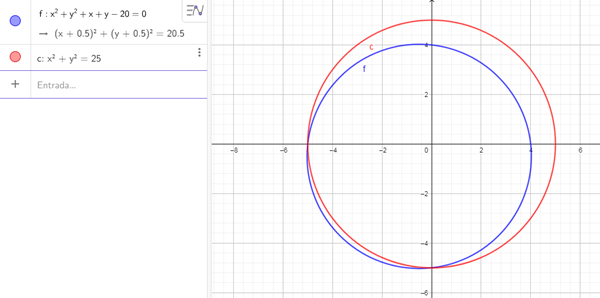
Muy bien, ahora vamos a resolverlo analíticamente...
$$\begin{align}&c1:x^2+y^2=25 \to x^2+y^2-25=0\\&c2:x^2+y^2+x+y-20=0\\&c1=c2\\& x^2+y^2-25=x^2+y^2+x+y-20\\&x+y=-5 \to y=-x-5 ......(*)\\&\text{Los puntos de intersección estarán sobre esa recta, veamos cuales cumplen con la circunferencia}\\&c1: x^2+(-x-5)^2=25 \\&x^2+x^2+10x+25=25 \\&2x^2+10x=0\\&2x(x+5)=0 \\&\text{Dos opciones}\\&x_1=0 \to \text{Reemplazo en (*) para averiguar 'y'} \to y=-5\\&x_2=-5 \to \text{Reemplazo en (*) para averiguar 'y'} \to y=0\\&\text{Veamos si esos puntos también pertenecen a la expresión c2}\\&c2:x^2+y^2+x+y-20=0\\&(0,-5): \to 0^2+(-5)^2+0+(-5)-20=0 \ Cumple!\\&(-5,0): \to (-5)^2+0^2+(-5)+0-20=0 \ Cumple!\\&\text{Ya se veía en el gráfico que esos eran los valores, pero siempre hay que verificar...}\end{align}$$Salu2