¿Qué fuerza mínima se requiere?
Una caja cúbica está llena de arena y pesa 892N. Se desea que la caja “ruede” empujándola horizontalmente en uno de los bordes superiores.
a.- ¿Qué fuerza mínima se requiere?
b.- ¿Qué coeficiente mínimo de fricción estática se requiere?
c.- ¿Hay una manera más eficiente de hacer que la caja ruede?
De ser así, halle la menor fuerza posible que debería aplicarse directamente a la caja.
1 respuesta
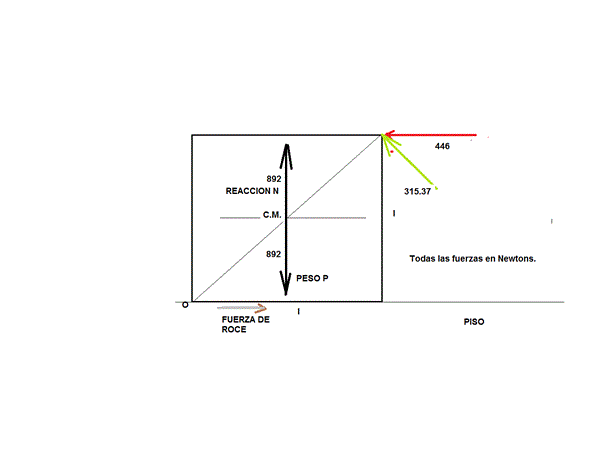
Para analizarlo toma un plano paralelo a una de las caras del cubo que pase por el C.M.y trabajarias sobre ese plano. O sea sobre una superficie cuadrada de lado l que concentren su C.M. el peso total del cubo = 892 N.
Traza el cuadrado y el C.M.. el punto O seria el centro de giro y el borde B el punto de aplicación de la fuerza F horizontal que te piden.
La condición limite ( que la caja ruede) esta fijada por una ecuación de momentos.
Mo = F l + l/2 N - P l/2 = 0...............de aqui deducis la Fmin. A partir de la cual la caja comienza a girar. Pero cuando eso ocurre la reacción normal N se te corre al punto de apoyo O... con lo cual su momento asociado desaparece.
Mo= 0= Fl = Pl/2 ........... o sea Fmin > P/2 > 892/2 = 446 N.
Como F min = mu ( min) x N ,tendrias
mu ( min) x N x l = Pl/2 ....................y como P= N ( en modulo) simplificando te queda: mu ( min) = 0.50
Con referencia a este esfuerzo mínimo aplicado en el borde = Fmin.= lo podes reducir aun mas considerando que aplicas la fuerza sobre B pero perpendicularmente a la diagonal del cuadrado de analisis........................
con lo cual F' ( min) = F( min) / V2 = 315.3 N.
Te acompaño croquis.
