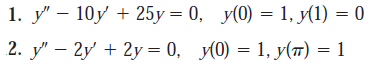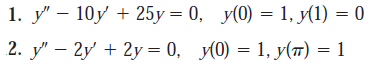Ejercicios de ecuaciones diferenciales lineales

No son valores en la frontera sino valore iniciales en ambos ejemplos (observa que todos son valores para y).

1.  Auxiliar:  m^2-10m+25=0;  Baskara:

[10+-√ (100-100)) / 2;  m=5;  dos valores iguales.

y=C1e^5x + C2xe^5x;  Reemplazo y quedan dos ecuaciones con dos incógnitas:

1 = C1 + 0C2;  C1=1;

0 = C1e^5 + C2e^5;  C2= (-1)

y = e^5x - xe^5x;  o:  y = e^5x * (1-x).

2.  Auxiliar:  m^2 -2m+2=0;  Baskara:

[2 +-√ (4-8)] / 2;  1+-i;  Resultado complejo:

y = e^x (C1Senx + C2Cosx).  Reemplazo:

1= e^0* (C1Sen0 + C2Cos0);  1= C2;

1= e^π * (C1Senπ + C2Cosπ);  1 = e^π *(-C2);  C2= (-e)^(-π);

Con estos valores iniciales obtengo dos valores posibles para C2 y ninguno para C1, por lo que no puedo llegar a la solución.