Cociente polinomios con dos variables.
En un cociente entre polinomios de tercer grado incompletos con dos variables.
¿Se puede comprobar que se ha operado bien dando una pareja de valores cualquiera y sustituyéndolos en la expresión final e inicial?
2 Respuestas
Respuesta de Pilar Valenzuela
2
Respuesta
2
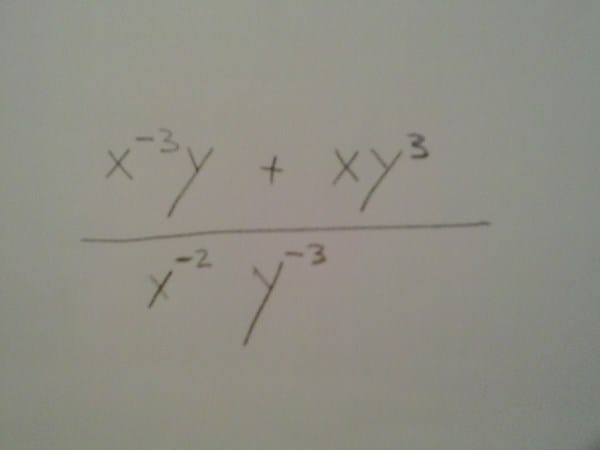
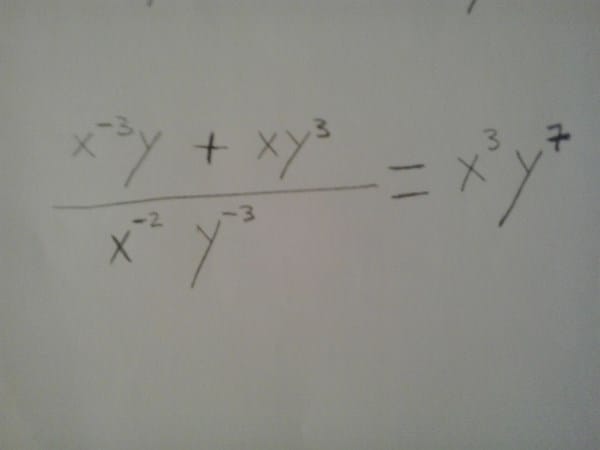

Comentario borrado por el autor - Anónimo
Igualmente a como está planteada la pregunta, eso es condición necesaria pero no suficiente. Habría que armar el caso, pero estoy 99% seguro que la pregunta es Falsa (no me metí a responderla porque creo que no está del todo bien formulada la pregunta, pero creo que con que un par de valores cumplan la condición, no asegura que todo el cociente sea correcto) - Anónimo
Pues si, el sistema tendrá que tener un valor exacto para cada una de las variables, pero siempre he comprobado ecuaciones minimizadas de esta forma y hasta ahorita mientras cumpla la igualdad, me ha resultado verdadero.Si se tendría que ver la ecuación para confirmar la hipótesis. Gracias por tu comentario. - Pilar Valenzuela