Hallar la ecuación de la circunferencia

Tienes que hallar el incentro de ese triangulo.

Para ello primero te recomiendo graficar las rectas para tener una idea de como se ve el dibujo

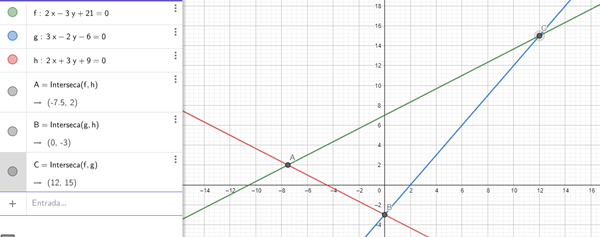
Para hallar el incentro debes hallar dos bisectrices. Las bisectrices son rectas que dividen un angulo a la mitad. Digamos entonces la recta h y la recta f, primero debes usar la fórmula de angulo entre dos rectas

$$\begin{align}&tg \alpha=\frac{m_2-m_1}{1+m_2m_1}\end{align}$$

Con esa formula y despejando alfa obtienes el angulo entre las dos rectas(m1 debe ser la recta que esta encima de la otra)

Luego divides ese angulo alfa entre dos. Y usando

$$\begin{align}&Tg \alpha=m\end{align}$$

obtienes la pendiente de la bisectriz que divide a la mitad el angulo formado por h y F

Con esa pendiente y el punto A (porque la bisectriz debe pasar por la intersección entre las dos rectas) obtienes la ecuación de una bisectriz.

Haces lo mismo con otro par de lados y obviamente el punto que vas a usar en la ecuación punto pendiente va a cambiar, igual que las pendientes de las rectas

Con dos bisectrices haces un sistema de ecuaciones y obtienes las coordenadas del incentro. Ese va a ser el centro de la circunferencia

$$\begin{align}&(x-h)^2+(y-k)^2=r^2\end{align}$$

H y k son las coordenadas del centro, pero no tenemos el radio.

Para hallar el radio debes hallar intersección de una bisectriz con el lado del triangulo opuesto.

En el ejemplo de la recta f y h, debes hallar la intersección de la bisectriz con la recta g.

Haces la distancia entre dos puntos entre el centro y esa intersección y obtienes el radio. Con eso tienes la ecuación de la circunferencia