El teorema de Torricelli nos dice que
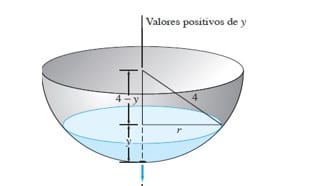
$$\begin{align}&A(y)y'=-a \sqrt{2gy}\end{align}$$A(y) es el area de la seccion transversal(cortamos esa esfera en circulos) y a es el area del orificio por donde sale el agua.
Para hallar el area de la seccion transversal pues depende de la altura.
$$\begin{align}&A= \pi r^2\\&\text{Usando el teorema de pitagoras para hallar el radio de esas circunferencias tenemos}\\&16=r^2+(4-y)^2\\&r^2=8y-y^2\\&\\&A= \pi (8y-y^2)\\&\\&\text{Sustituyamos en la ec diferencial, el valor del orificio lo hacemos luego, es cte al fin y al cabo}\\&\\& \pi (8y-y^2)y'=-a \sqrt{2gy}\\&\int \frac{\pi (8y-y^2)}{\sqrt{2gy}}dy=-a \int \, dt\\&\frac{\pi}{\sqrt{2g}}\int \frac{8y}{\sqrt{y}}-\frac{y^2}{\sqrt{y}} dy=-a \int \, dt\\&\frac{\pi}{\sqrt{2g}} \int 8 \sqrt{y} - y^\frac{3}{2}dy=-a \int \, dt\\&\frac{\pi}{\sqrt{2g}} \bigg(\frac{16}{3} y^\frac{3}{2}-\frac{2}{5} y^\frac{5}{2}\bigg)=-at\\&\end{align}$$Vamos a poner limites de integracion, en t=0 el tanque esta lleno, por lo que el valor de y es el radio de esa tanque y(0)=4, y en t=to el tanque esta vacio y(to)=0
$$\begin{align}&\frac{\pi}{\sqrt{2g}} \bigg(\frac{16}{3} y^\frac{3}{2}-\frac{2}{5} y^\frac{5}{2}\bigg) \bigg]_4^0=-at\bigg]_0^{t_o}\\&\frac{-448 \pi}{15 \sqrt{2g}}=-a t_o\\&\text{Hallemos el valor del area del orificio}\\&d=1\\&r=\frac{1}{2} pulgadas=\frac{1}{24}pies\\&a=\frac{\pi}{576}\\&\text{sustituyendo}\\&\frac{448 \pi}{15 \sqrt{2g}}=\frac{\pi}{576}t_o\\&\text{Tomando g=32 pies /s}\\&t_0=2150.4s=35.83 min\\&\text{35 min son 2100s entonces 2150.4-2100=50.4s Por lo que .83 min equivalen a 50.4s}\\&\end{align}$$La respuesta final es35 min 50s