Como puedo hacer esta demostración de matrices en geometría vectorial
Sea la matriz A, con elementos no negativos, los cuales cumplen con las siguientes propiedades ; adjunto imagen para una mejor comprensión
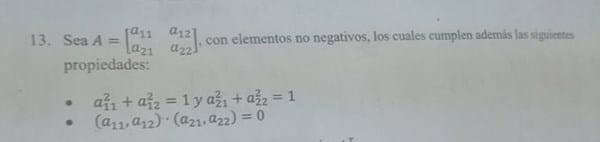
.
Respuesta de Alejandro Salazar
1


