Quien solución de calculo diferencial
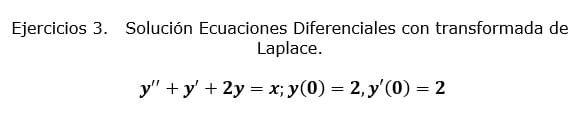
Quien solución de calculo diferencial y gracias por la explicación del desarrollo del respectivo ejercicio
Gracias por todo.
Quien solución de calculo diferencial y gracias por la explicación del desarrollo del respectivo ejercicio
Gracias por todo.
Quien solución de calculo diferencial y gracias por la explicación del desarrollo del respectivo ejercicio
1 Respuesta
Respuesta de Karl Mat
