¿Qué denota x-a en una serie de Taylor?
Estuve leyendo sobre series de Taylor y entiendo bien lo de los coeficientes, según entiendo a partir de la forma de la serie de Taylor si se deriva "n" numero de veces la serie se obtiene como primer termino el coeficiente del enésimo termino multiplicado por "n!", por eso se divide por "n!" en la forma general, pero no entiendo que representa el:
$$\begin{align}&(x-1)^n\end{align}$$de:
$$\begin{align}&f(x)=\sum_{i=0}^{inf} C_n(x-a)^n\end{align}$$¿Qué representa?
1 Respuesta
NOTA: Cuando diga serie, es el polinomio de grado "infinito", si digo polinomio de taylor, es el polinomio de grado n
El a en si representa el punto desde donde se va a evaluar el polinomio, se podría haber colocado por y listo, pero representa una ventaja el colocar el (x-a)^n, y es que si te das cuenta
$$\begin{align}&f^{(k)}(x) = \sum_{n= 0}^{\infty} C_n\frac{n!}{(n-k)!}(x-a)^{(n-k)}\end{align}$$Osea, la derivada k de f te da la expresi'on de la derecha, lo de los factoriales pues se obtiene practicamente observando el patron, puedes comprobar con boli que en verdad se cumple. (Prueba con un polinomio generico( a0+a1x+a2x^2+a3x^3+...) y ve que sucede con los terminos al multiplicar).
Que sucede cuando evaluamos en a la expresion de arriba
$$\begin{align}&f^{(k)}(a) = \sum_{n= 0}^{\infty} C_n\frac{n!}{(n-k)!}(a-a)^{(n-k)}\\&f^{(k)}(a) = C_k\frac{k!}{0!}\\&C_k = \frac{f^{(k)}(a) }{k!}\end{align}$$Pues que claro a la derecha (a-a) es 0, excepto cuando n = k, que primero se realizaria la potencia, antes de realizar la sustitucion x=a. Te quedaria 1 y ese es el termino que te queda. Asi pues comprobamos lo de los factoriales.
Que ventaja nos da (x-a) pues que si derivas que veces, el único termino que te va a quedar al evaluar en x=a sera pues lo que nos dio antes. Otra cosa, si recuerdas si tu tienes una función f(x-b), lo que tienes es una función desplazada. El (x-a) en si lo que hace es centrar tu polinomio en a y hacer tus aproximaciones a partir de ahi. (abajo se puede ver que las aproximaciones estan hechas centradas en x=0, entonces a =0)
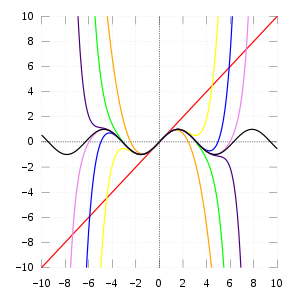
El polinomio de taylor lo que busca es aproximar la función, en el limite cuando el grado del polinomio tiende a infinito, la función y el polinomio son iguales (bajo ciertas condiciones, por ejm la serie de taylor de ln(1+x) converge en un intervalo concreto, pero si te sales de el, ya los valores son incorrectos, si te interesa, busca un poco sobre el radio de convergencia.).
Claro, si la serie converge para todo x, pues la verdad da igual, pero no siempre es así (radio de convergencia). Entonces encontrar un a que te permita hallar un valor en concreto es bueno. Por otro lado, si tienes un polinomio de taylor, dependiendo el valor de a que elijas, si quieres hallar una aproximación de f(b) para un cierto b, pues elegir un a "cercano" es bueno, ya que necesitas menor grado de tu polinomio para tener resultados decentes.
Cualquier cosa me dices, igual me fui por un camino que no era el que querías, de todas formas espero haber sido de ayuda.
Al hacer la derivada k-esima, n no empieza en 0, empieza en k, porque al derivar los términos ctes de la serie van desapareciendo.
