Problema geometría analitica
Un problema de telescopio parabólico-hiperbólico
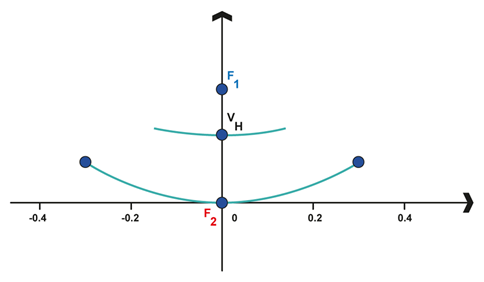
El siguiente diagrama representa un diseño experimental de un telescopio parabólico-hiperbólico. Se sabe que el diámetro del espejo parabólico es de 0.6 metros y tiene una profundidad de 9 cm, mientras que el diámetro del espejo hiperbólico es de 0.3 metros.
De acuerdo con el sistema de coordenadas propuesto. ¿En dónde se ubica el foco común de ambos espejos? Expresa tu resultado en metros.
1 respuesta
La ecuación canónica de una parábola con vértice en (0,0) y es transversal al eje Y es:
2py = x²
Donde p es la distancia del foco a la directriz.
Luego p/2 es la distancia del vértice al foco y el punto F1 será (0, p/2)
Y ya solo falta que dicha parábola pase por el punto del borde del espejo que nos facilitan.
Como el diámetro es 0.6m la coordenada x será 0.3. La profundidad es 9cm=0.09m, eso es la altura del punto tal como está dispuesta la figura.
Luego el punto del borde es (0.3, 0.09) y para pertenecer a la parábola debe ser:
2p(0.09) = 0.3² = 0.09
2p = 1
p= 1/2
F1=(0, (1/2)/2) = (0, 1/4)
Ya va expresado en metros, es (0m, 0.25m)
El espejo hiperbólico es un mero adorno, no nos dan suficientes datos como para que hubiera ayudado a resolver la posición del foco. Hubiera dado lo mismo que dibujaran ahí un pájaro volando.
Y eso es todo.
