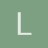A integrar...
Hola que tal, estoy preparando un final de análisis matemático (curso en la UNLP informática) y me surgieron dos dudas que no se me ocurre como solucionarlas. Ambas tienen que ver con integración indefinida.
Sea "S" el símbolo de la integral y "e" el exponencial y "^" potencia.
Las ecucaciones a integrar son las siguientes:
1) S e^(- x^2)
2) S x^(1/2) e^(1/2)
Bueno, la verdad probé de varias maneras pero no sé como integrarlo, por lo tanto, no puedo hallar primitivas, desde ya muchas gracias si me puedes ayudar.
Sea "S" el símbolo de la integral y "e" el exponencial y "^" potencia.
Las ecucaciones a integrar son las siguientes:
1) S e^(- x^2)
2) S x^(1/2) e^(1/2)
Bueno, la verdad probé de varias maneras pero no sé como integrarlo, por lo tanto, no puedo hallar primitivas, desde ya muchas gracias si me puedes ayudar.
1 Respuesta
Respuesta de eudemo
1