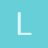Lim x--> 0 |x|sen (1/x) existe?
Tengo la duda de si ese limite existe o no. Nuestro profesor dice que el limite es cero, pero yo pienso que es así:
Lim |x|sen(1/x)
x->0
Multiplico y divido por 1/x:
Lim |x|.(1/x) sen(1/x) / (1/x)
x->0
Me queda:
Lim |x|/x
x->0
El cual no existe pues por limites laterales tiene un valor diferente.
Nuestro profesor explica algo así (no lo recuerdo muy bien):
-1 < sen(1/x) < 1
Multiplica |x| en toda la expresión:
-|x| < |x|sen(1/x) < |x|
Y bueno, de ahí no recuerdo que más hace...
¿Me ayudas?
Lim |x|sen(1/x)
x->0
Multiplico y divido por 1/x:
Lim |x|.(1/x) sen(1/x) / (1/x)
x->0
Me queda:
Lim |x|/x
x->0
El cual no existe pues por limites laterales tiene un valor diferente.
Nuestro profesor explica algo así (no lo recuerdo muy bien):
-1 < sen(1/x) < 1
Multiplica |x| en toda la expresión:
-|x| < |x|sen(1/x) < |x|
Y bueno, de ahí no recuerdo que más hace...
¿Me ayudas?
Respuesta de Valero Angel Serrano Mercadal
1
No entiendo como llegas a esa conclusión. Es como si supusieras que el límite cuando por -> 0 de
sen(1/x)/(1/x) = 1
Pero fíjate bien y haciendo correctamente la división verás que sen(1/x)/(1/x) = x·sen(1/x) que tiene limite 0 cuando x->0
Lo que hace tu profesor está bien:
De -|x| < |x|sen(1/x) < |x| tendremos que cuando x -> 0 los extremos -|x| y |x| tienden a cero y por lo tanto lo que hay encajonado dentro |x|sen(1/x) también tiende a cero. Es el teorema de los intervalos encajados que no sé si habrás dado ya.
De todas formas, para estar más seguro, puedes acudir a la definición de límite.
Limite de |x|sen(1/x)=0 cuando x-->0 si y solo si para todo epsilon>0 existe un delta>0 tal que si |x-0| < delta ==> ||x|sen(1/x) - 0|< epsilon
Dado cualquier epsilon tan pequeño como queramos basta que tomemos delta = epsilon y vamos a ver como se cumple la condición del limite.
Por la elección será |x| < delta = epsilon y usaremos tambien que |sen(1/x)| <= 1 siempre
||x|sen(1/x)| < |epsilon sen(1/x)| = |epsilon||sen(1/x)|<= |epsilon| = epsilon
luego se cumple la condición y el límite es cero.
Y eso es todo. Espero que te haya quedado claro. No olvides puntuar y cerrar la pregunta.
sen(1/x)/(1/x) = 1
Pero fíjate bien y haciendo correctamente la división verás que sen(1/x)/(1/x) = x·sen(1/x) que tiene limite 0 cuando x->0
Lo que hace tu profesor está bien:
De -|x| < |x|sen(1/x) < |x| tendremos que cuando x -> 0 los extremos -|x| y |x| tienden a cero y por lo tanto lo que hay encajonado dentro |x|sen(1/x) también tiende a cero. Es el teorema de los intervalos encajados que no sé si habrás dado ya.
De todas formas, para estar más seguro, puedes acudir a la definición de límite.
Limite de |x|sen(1/x)=0 cuando x-->0 si y solo si para todo epsilon>0 existe un delta>0 tal que si |x-0| < delta ==> ||x|sen(1/x) - 0|< epsilon
Dado cualquier epsilon tan pequeño como queramos basta que tomemos delta = epsilon y vamos a ver como se cumple la condición del limite.
Por la elección será |x| < delta = epsilon y usaremos tambien que |sen(1/x)| <= 1 siempre
||x|sen(1/x)| < |epsilon sen(1/x)| = |epsilon||sen(1/x)|<= |epsilon| = epsilon
luego se cumple la condición y el límite es cero.
Y eso es todo. Espero que te haya quedado claro. No olvides puntuar y cerrar la pregunta.
Si, es el teorema del "emparedado", como lo llamamos aquí, tienes razón. En el examen lo olvidé.
Respecto a como digo que Lim x->0 sen (1/x) / (1/x)= 1, lo digo por la "identidad" que dice que
Lim sen (x) / x = 1
x->0
Muchísimas gracias por tu respuesta, me ha quedado claro como se hace. Lo que no me queda claro es por qué no se hace con la identidad que estoy mencionando más arriba. Pero muchísimas gracias!
Respecto a como digo que Lim x->0 sen (1/x) / (1/x)= 1, lo digo por la "identidad" que dice que
Lim sen (x) / x = 1
x->0
Muchísimas gracias por tu respuesta, me ha quedado claro como se hace. Lo que no me queda claro es por qué no se hace con la identidad que estoy mencionando más arriba. Pero muchísimas gracias!
